
【题目】已知函数![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)对于曲线上的不同两点![]() ,如果存在曲线上的点
,如果存在曲线上的点![]() ,且
,且![]() 使得曲线在点
使得曲线在点![]() 处的切线
处的切线![]() ,则称
,则称![]() 为弦
为弦![]() 的伴随直线,特别地,当
的伴随直线,特别地,当![]() 时,又称
时,又称![]() 为
为![]() 的
的![]() —伴随直线.
—伴随直线.
①求证:曲线![]() 的任意一条弦均有伴随直线,并且伴随直线是唯一的;
的任意一条弦均有伴随直线,并且伴随直线是唯一的;
②是否存在曲线![]() ,使得曲线
,使得曲线![]() 的任意一条弦均有
的任意一条弦均有![]() —伴随直线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由.
—伴随直线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由.
【答案】(Ⅰ)![]() …………………………………… 2分
…………………………………… 2分
当![]() ,
,![]() ,函数
,函数![]() 在
在![]() 内是增函数,
内是增函数,
∴函数![]() 没有极值。 ……………………………… 3分
没有极值。 ……………………………… 3分
当![]() 时,令
时,令![]() ,得
,得![]() 。
。
当![]() 变化时,
变化时,![]() 与
与![]() 变化情况如下表:
变化情况如下表:
|
|
|
|
| + | 0 | - |
| 单调递增 | 极大值 | 单调递减 |
∴当![]() 时,
时,![]() 取得极大值
取得极大值![]() 。
。
综上,当![]() 时,
时,![]() 没有极值;
没有极值;
当![]() 时,
时,![]() 的极大值为
的极大值为![]() ,没有极小值。 ……………5分
,没有极小值。 ……………5分
(Ⅱ)(ⅰ)设![]() 是曲线
是曲线![]() 上的任意两点,要证明
上的任意两点,要证明
![]() 有伴随切线,只需证明存在点
有伴随切线,只需证明存在点![]() ,使得
,使得
![]() ,且点
,且点![]() 不在
不在![]() 上。 ……………………7分
上。 ……………………7分
∵![]() ,即证存在
,即证存在![]() ,使得
,使得![]() ,即
,即![]() 成立,且点
成立,且点![]() 不在
不在![]() 上。 …………………8分
上。 …………………8分
以下证明方程![]() 在
在![]() 内有解。
内有解。
记![]() ,则
,则![]() 。
。
令![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() 内是减函数,∴
内是减函数,∴![]() 。
。
取![]() ,则
,则![]() ,即
,即![]() 。……9分
。……9分
同理可证![]() 。∴
。∴![]() 。
。
∴函数![]() 在
在![]() 内有零点。
内有零点。
即方程![]() 在
在![]() 内有解
内有解![]() 。………………10分
。………………10分
又对于函数![]() 取
取![]() ,则
,则![]()
可知![]() ,即点Q不在
,即点Q不在![]() 上。
上。
![]() 是增函数,∴
是增函数,∴![]() 的零点是唯一的,
的零点是唯一的,
即方程![]() 在
在![]() 内有唯一解。
内有唯一解。
综上,曲线![]() 上任意一条弦均有伴随切线,并且伴随切线是唯一的。…… 11分
上任意一条弦均有伴随切线,并且伴随切线是唯一的。…… 11分
(ⅱ)取曲线C:![]() ,则曲线
,则曲线![]() 的任意一条弦均有
的任意一条弦均有![]() 伴随切线。
伴随切线。
证明如下:设![]() 是曲线C上任意两点
是曲线C上任意两点![]() ,
,
则![]() ,
,
又![]() ,
,
即曲线C:![]() 的任意一条弦均有
的任意一条弦均有![]() 伴随切线。
伴随切线。
【解析】略


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知数据x1,x2,x3,…,xn是普通职工n(n≥3,n∈N*)个人的年收入,设这n个数据的中位数为x,平均数为y,方差为z,如果再加上世界首富的年收入xn+1,则这n+1个数据中,下列说法正确的是
A. 年收入平均数大大增大,中位数一定变大,方差可能不变
B. 年收入平均数大大增大,中位数可能不变,方差变大
C. 年收入平均数大大增大,中位数可能不变,方差也不变
D. 年收入平均数可能不变,中位数可能不变,方差可能不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱锥![]() 中底面边长为
中底面边长为![]() ,侧棱PA与底面ABCD所成角的正切值为
,侧棱PA与底面ABCD所成角的正切值为![]() .
.
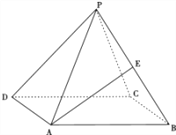
(I)求正四棱锥![]() 的外接球半径;
的外接球半径;
(II)若![]() 是
是![]() 中点,求异面直线
中点,求异面直线![]() 与
与![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4, ![]() ,AB=2CD=8.
,AB=2CD=8.
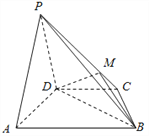
(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)当M点位于线段PC什么位置时,PA∥平面MBD?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】3名志愿者在10月1号至10月5号期间参加社区服务工作.
(1)若每名志愿者在这5天中任选一天参加社区服务工作,且各志愿者的选择互不影响,求3名志愿者恰好连续3天参加社区服务工作的概率;
(2)若每名志愿者在这5天中任选两天参加社区服务工作,且各志愿者的选择互不影响,记![]() 表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量
表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用![]() (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度![]() (单位:
(单位: ![]() )满足关系
)满足关系![]() ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设![]() 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用![]() 达到最小,并求最小值。
达到最小,并求最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com