
分析 (1)函数f(1)=$\frac{m}{1+n}=2$.所以m=2+2n,f(x)=$\frac{(2+2n)x}{{x}^{2}+n}$,又f(x)在x=1处取得极值,f$′(1)=\frac{2{n}^{2}-2}{(1+n)^{2}}=0$,n=1,则m=4
(2)由f(x)-k=0,得k=f(x),由(1)得f$′(x)=\frac{4-4{x}^{2}}{(1+{x}^{2})^{2}}$,令f′(x)=0,得x=±1.求出单调区间,根据图象即可求解.
(3)对于任意x1∈R,总存在x2∈[-1,0],使得g(x2)≤f(x1),只需g(x2)min≤f(x1)min,即当x∈[-1,0]时,x2-2ax+a≤-2恒成立,只需$\left\{\begin{array}{l}{(-1)^{2}-2a×(-1)+a≤-2}\\{{0}^{2}-2a×0+a≤-2}\end{array}\right.$,解得a.
解答 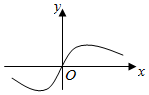 解:(1)因为函数f(1)=$\frac{m}{1+n}=2$.
解:(1)因为函数f(1)=$\frac{m}{1+n}=2$.
所以m=2+2n,f(x)=$\frac{(2+2n)x}{{x}^{2}+n}$,
又f(x)在x=1处取得极值,
f$′(x)=\frac{(2+2n)({x}^{2}+n)-(2+2n)x•2x}{({x}^{2}+n)^{2}}$=$\frac{2n+2{n}^{2}-(2+2n){x}^{2}}{({x}^{2}+n)^{2}}$,
f$′(1)=\frac{2{n}^{2}-2}{(1+n)^{2}}=0$,n=1,则m=4,
经检验满足题意,
所以$f(x)=\frac{4x}{{{x^2}+1}}=\frac{4}{{x+\frac{1}{x}}}$;
(2)由f(x)-k=0,得k=f(x),
由(1)得f$′(x)=\frac{4-4{x}^{2}}{(1+{x}^{2})^{2}}$,
令f′(x)=0,得x=±1.
当x变化时,f′(x),f(x)的变化情况如下表:
| x | (-∞,-1) | -1 | (-1,1) | 1 | (1,+∞) |
| f'(x) | - | 0 | + | 0 | - |
| f(x) | 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
点评 本题考查了导数的应用,根的个数的判定,存在性问题,考查了转化思想、数形结合思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2k-1 | B. | 2k | C. | 2k-1 | D. | 2k+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如下图是函数y=Asin(ωx+φ)+k(|φ|<$\frac{π}{2}$)在一个周期内的图象,那么这个函数的一个解析式是f(x)=3sin(2x+$\frac{π}{3}$)-1.
如下图是函数y=Asin(ωx+φ)+k(|φ|<$\frac{π}{2}$)在一个周期内的图象,那么这个函数的一个解析式是f(x)=3sin(2x+$\frac{π}{3}$)-1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,一条巡逻船由南向北行驶,在A处测得山顶P在北偏东15°(∠BAC=15°)方向上,匀速向北航行20分钟到达B处,测得山顶P位于北偏东60°方向上,此时测得山顶P的仰角60°,若山高为$2\sqrt{3}$千米,
如图,一条巡逻船由南向北行驶,在A处测得山顶P在北偏东15°(∠BAC=15°)方向上,匀速向北航行20分钟到达B处,测得山顶P位于北偏东60°方向上,此时测得山顶P的仰角60°,若山高为$2\sqrt{3}$千米,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com