
分析 (1)由题意,|NM|+|NF|=6>|FM|,由椭圆定义知,圆心N的轨迹为椭圆,且2a=6,c=1,即可求曲线C的方程;
(2)$|{OS}|•|{OT}|=|{{x_S}{x_T}}|=|{\frac{{{x_0}{y_1}-{x_1}{y_0}}}{{{y_1}-{y_0}}}•\frac{{{x_0}{y_1}+{x_1}{y_0}}}{{{y_1}+{y_0}}}}|=|{\frac{{{x_0}^2{y_1}^2-{x_1}^2{y_0}^2}}{{{y_1}^2-{y_0}^2}}}|$,即可证明结论.
解答 解:(1)因为点F(1,0)在M:(x+1)2+y2=36内,所以圆N内切于圆M,则|NM|+|NF|=6>|FM|,
由椭圆定义知,圆心N的轨迹为椭圆,且2a=6,c=1,则a2=9,b2=8,
所以动圆圆心N的轨迹方程为$\frac{x^2}{9}+\frac{y^2}{8}=1$.
(2)设P(x0,y0),A(x1,y1),S(xS,0),T(xT,0),则B(x1,-y1),
由题意知x0≠±x1.则${k_{AP}}=\frac{{{y_1}-{y_0}}}{{{x_1}-{x_0}}}$,直线AP方程为y-y1=kAP(x-x1),
令y=0,得${x_S}=\frac{{{x_0}{y_1}-{x_1}{y_0}}}{{{y_1}-{y_0}}}$,同理${x_T}=\frac{{{x_0}({-{y_1}})-{x_1}{y_0}}}{{({-{y_1}})-{y_0}}}=\frac{{{x_0}{y_1}+{x_1}{y_0}}}{{{y_1}+{y_0}}}$,
于是$|{OS}|•|{OT}|=|{{x_S}{x_T}}|=|{\frac{{{x_0}{y_1}-{x_1}{y_0}}}{{{y_1}-{y_0}}}•\frac{{{x_0}{y_1}+{x_1}{y_0}}}{{{y_1}+{y_0}}}}|=|{\frac{{{x_0}^2{y_1}^2-{x_1}^2{y_0}^2}}{{{y_1}^2-{y_0}^2}}}|$,
又P(x0,y0)和A(x1,y1)在椭圆$\frac{x^2}{9}+\frac{y^2}{8}=1$上,
故${y_0}^2=8({1-\frac{{{x_0}^2}}{9}}),{y_1}^2=8({1-\frac{{{x_1}^2}}{9}})$,则${y_1}^2-{y_0}^2=\frac{8}{9}({{x_0}^2-{x_1}^2}),{x_0}^2{y_1}^2-{x_1}^2{y_0}^2=8{x_0}^2({1-\frac{{{x_1}^2}}{9}})-8{x_1}^2({1-\frac{{{x_0}^2}}{9}})=8({{x_0}^2-{x_1}^2})$.
所以$|{OS}|•|{OT}|=|{\frac{{{x_0}^2{y_1}^2-{x_1}^2{y_0}^2}}{{{y_1}^2-{y_0}^2}}}|=|{\frac{{8({{x_0}^2-{x_1}^2})}}{{\frac{8}{9}({{x_0}^2-{x_1}^2})}}}|=9$.
点评 本题考查椭圆的定义与方程,考查定值的证明,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{2}$ | B. | 3 | C. | $\frac{9}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
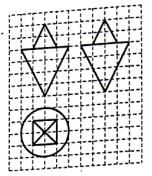
| A. | $\frac{16}{3}(π+1)$ | B. | $\frac{8}{3}(2π+1)$ | C. | 8(2π+1) | D. | 16(π+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
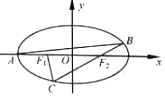 如图,设点A,F1,F2分别为椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左顶点和左,右焦点,过点A作斜率为k的直线交椭圆于另一点B,连接BF2并延长交椭圆于点C.
如图,设点A,F1,F2分别为椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左顶点和左,右焦点,过点A作斜率为k的直线交椭圆于另一点B,连接BF2并延长交椭圆于点C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(1,+∞) | B. | (-∞,-2) | C. | (1,+∞) | D. | (-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com