
 Ϊ��սij���˶��ᣬij���������齨��һ����4�����˶�Ա��2��Ů�˶�Ա��ɵ�6�˴����Ӳ����б�սѵ����
Ϊ��սij���˶��ᣬij���������齨��һ����4�����˶�Ա��2��Ů�˶�Ա��ɵ�6�˴����Ӳ����б�սѵ�������� ��1�������6�������ѡ��2�ˣ�ѡ����2����������1��Ů�˶�Ա�Ļ����¼����������Ӧ�ĸ���ֵ��
��2��������Ŀ�е����ݣ�������Ҷͼ������ס����˶�Ա��ƽ���ɼ��뷽��Ƚϴ�С���ɵó����ۣ�
��� �⣺��1����6�������ѡ��2�ˣ�ѡ����2����������1��Ů�˶�Ա�ĸ���Ϊ
P=1-$\frac{{C}_{4}^{2}}{{C}_{6}^{2}}$=1-$\frac{6}{15}$=$\frac{3}{5}$��
��2��������Ŀ�е����ݣ�������Ҷͼ��ͼ��ʾ��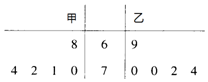
����˶�Ա��ƽ���ɼ�Ϊ$\overline{{x}_{1}}$������Ϊ${{s}_{1}}^{2}$��
���˶�Ա��ƽ���ɼ�Ϊ$\overline{{x}_{2}}$������Ϊ${{s}_{2}}^{2}$��
�ɵ�$\overline{{x}_{1}}$=$\frac{1}{5}$����68+70+71+72+74��=71��
$\overline{{x}_{2}}$=$\frac{1}{5}$����69+70+70+72+74��=71��
${{s}_{1}}^{2}$=$\frac{1}{5}$��[��68-71��2+��70-71��2+��71-71��2+��72-71��2+��74-71��2]=4��
${{s}_{2}}^{2}$=$\frac{1}{5}$��[��69-71��2+��70-71��2+��70-71��2+��72-71��2+��74-71��2]=3.2��
��$\overline{{x}_{1}}$=$\overline{{x}_{2}}$��${{s}_{1}}^{2}$��${{s}_{2}}^{2}$�������˶�Ա�ijɼ����ȶ���
���� ���⿼���˹ŵ���͵ĸ����뾥Ҷͼ��ƽ�����ͷ����Ӧ�����⣬�ǻ�����Ŀ��


 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� | 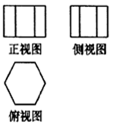 | C�� | 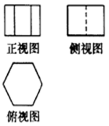 | D�� | 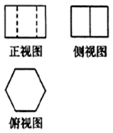 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
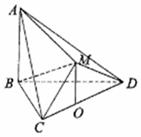 ��ͼ���ڶ�����ABCDM�У���BCD�ǵȱ������Σ���CMD�ǵ���ֱ�������Σ���CMB=90�㣬ƽ��CMD��ƽ��BCD��AB��ƽ��BCD����OΪCD���е㣬����OM��
��ͼ���ڶ�����ABCDM�У���BCD�ǵȱ������Σ���CMD�ǵ���ֱ�������Σ���CMB=90�㣬ƽ��CMD��ƽ��BCD��AB��ƽ��BCD����OΪCD���е㣬����OM���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | b��a��c | C�� | c��a��b | D�� | b��c��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com