
分析 设出A.B.C,M.N.P的坐标,利用点差法,确定三条边所在直线的斜率,结合直线AB,BC,AC的斜率之和为-1,求得$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$+$\frac{1}{{k}_{3}}$的值.
解答 解:设A(x1,y1),B(x2,y2),C(x3,y3),
M(s1,t1),N(s2,t2),P(s3,t3),
由:2x12-y12=4,2x22-y22=4,两式相减,
得到2(x1-x2)(x1+x2)-(y1-y2)(y1+y2)=0,
x1+x2=2s1,y1+y2=2t1,k1=$\frac{{t}_{1}}{{s}_{1}}$,
∴kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=2•$\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$=2•$\frac{{s}_{1}}{{t}_{1}}$=$\frac{2}{{k}_{1}}$;
同理可得,kBC=2•$\frac{{s}_{2}}{{t}_{2}}$=$\frac{2}{{k}_{2}}$;
kAC=2•$\frac{{s}_{3}}{{t}_{3}}$=$\frac{2}{{k}_{3}}$.
由三边AB、BC、AC所在的直线的斜率均存在且均不为0,其和为-1,
即有kAB+kBC+kAC=$\frac{2}{{k}_{1}}$+$\frac{2}{{k}_{2}}$+$\frac{2}{{k}_{3}}$=-1,
则$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$+$\frac{1}{{k}_{3}}$=-$\frac{1}{2}$.
故答案为:-$\frac{1}{2}$.
点评 本题考查双曲线的方程和性质,主要考查点差法求斜率,考查运算能力,属于中档题.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
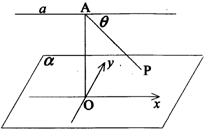 如图,已知直线a∥平面α,在平面α内有一动点P,点A是直线a上一定点,且AP与直线a所成角θ=$\frac{π}{4}$,点A到平面α的距离为2,若过点A作AO⊥α于点O,在平面α内,以过点O作直线a的平行线为x轴,以过点O作x轴的垂线为y轴建立直角坐标系,则动点P的轨迹方程为x2-y2=4..
如图,已知直线a∥平面α,在平面α内有一动点P,点A是直线a上一定点,且AP与直线a所成角θ=$\frac{π}{4}$,点A到平面α的距离为2,若过点A作AO⊥α于点O,在平面α内,以过点O作直线a的平行线为x轴,以过点O作x轴的垂线为y轴建立直角坐标系,则动点P的轨迹方程为x2-y2=4..查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
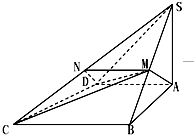 如图,四棱锥S-ABCD中,SA⊥底面ABCD,AB⊥AD,AD∥BC,SA=AB=BC=4,AD=2,M为SB的中点.
如图,四棱锥S-ABCD中,SA⊥底面ABCD,AB⊥AD,AD∥BC,SA=AB=BC=4,AD=2,M为SB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com