
四边形ABCD的边AD和BC的中点分别为E、F,
求证: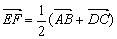
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
若直线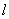 与曲线C满足下列两个条件:
与曲线C满足下列两个条件:
(i)直线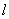 在点
在点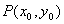 处与曲线C相切;(ii)曲线C在点
处与曲线C相切;(ii)曲线C在点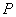 附近位于直线
附近位于直线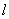 的两侧.则称直线
的两侧.则称直线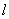 在点
在点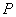 处“切过”曲线C.下列命题正确的是________(写出所有正确命题的编号).
处“切过”曲线C.下列命题正确的是________(写出所有正确命题的编号).
①直线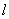 :y=0在点P(0,0)处“切过”曲线C
:y=0在点P(0,0)处“切过”曲线C :y=x3;
:y=x3;
②直线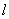 :x=-1在点P(-1,0)处“切过”曲线C:y=(x+1)2;
:x=-1在点P(-1,0)处“切过”曲线C:y=(x+1)2;
③直线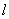 :y=x在点P(0,0)处“切过”曲线C:y=sin x;
:y=x在点P(0,0)处“切过”曲线C:y=sin x;
④直线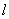 :y=x在点P(0,0)处“切过”曲线C:y=tan x;
:y=x在点P(0,0)处“切过”曲线C:y=tan x;
⑤直线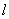 :y=x-1在点P(1,0)处“切过”曲线C:y=ln x.
:y=x-1在点P(1,0)处“切过”曲线C:y=ln x.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知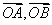 不共线,设
不共线,设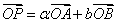 ,
,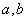 均为实数,且满足
均为实数,且满足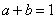 ,求证:
,求证: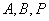 三点共线.
三点共线.
变式1:已知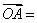 a + 2b,
a + 2b,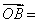 2a + 4b,
2a + 4b,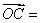 3a + 6b (其中a
3a + 6b (其中a  、b是两个任意非零向量) ,证明:A、B、C三点共线.
、b是两个任意非零向量) ,证明:A、B、C三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
一位幼儿园老师给班上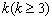 个小朋友分糖果.她发现糖果盒中原有糖果数为
个小朋友分糖果.她发现糖果盒中原有糖果数为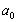 ,就先从别处抓2块糖加入盒中,然后把盒内糖果的
,就先从别处抓2块糖加入盒中,然后把盒内糖果的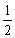 分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的
分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的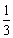 分给第二个小朋友;,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的
分给第二个小朋友;,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的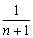 分给第
分给第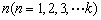 个小朋友.如果设分给第
个小朋友.如果设分给第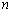 个小朋友后(未加入2块糖果前)盒内剩下的糖果数为
个小朋友后(未加入2块糖果前)盒内剩下的糖果数为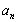 .
.
(1) 当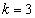 ,
,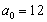 时,分别求
时,分别求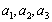 ;
;
(2) 请用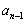 表示
表示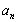 ;令
;令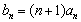 ,求数列
,求数列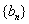 的通项公式;
的通项公式;
(3)是否存在正整数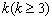 和非负整数
和非负整数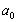 ,使得数列
,使得数列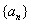
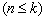 成等差数列,如果存在,请求出所有的
成等差数列,如果存在,请求出所有的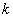 和
和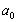 ,如果不存在,请说明理由.
,如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com