
| A. | 最大值为1 | B. | 图象关于直线x=-$\frac{π}{2}$对称 | ||
| C. | 既是奇函数又是周期函数 | D. | 图象关于点($\frac{3π}{4}$,0)中心对称 |
分析 根据题意逐一判断各个选项是否正确,从而得出结论.
解答 解:∵函数f(x)=sinxcos2x,当x=$\frac{3π}{2}$时,f(x)取得最大值为1,故A正确;
当x=-$\frac{π}{2}$时,函数f(x)=1,为函数的最大值,故图象关于直线x=-$\frac{π}{2}$对称;故B正确;
函数f(x)满足f(-x)=sin(-x)cos(-2x)=-sinxcos2x=-f(x),故函数f(x)为奇函数,
再根据f(x+2π)=sin(x+2π)cos[-2(x+2π)]=sinxcos2x,故f(x)的周期为2π,故C正确;
由于f($\frac{3π}{2}$-x)+f(x)=-cosx•cos(3π-2x)+sinxcos2x=cosxcos2x+sinxcos2x=cos2x(sinx+cosx)=0不一定成立,
故f(x)图象不一定关于点($\frac{3π}{4}$,0)中心对称,故D不正确,
故选:D.
点评 本题考查三角函数的对称性,考查了三角函数值域的解法,考查排除法在选择题中的应用,属于中档题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
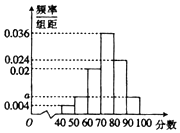 某高校在举行艺术类高考招生考试时,对100个考生进行了一项专业水平考试,考试成绩满分为100分,成绩出来后,老师对每个成绩段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]的人数进行了统计,丙得到如图所示的频率分布直方图.
某高校在举行艺术类高考招生考试时,对100个考生进行了一项专业水平考试,考试成绩满分为100分,成绩出来后,老师对每个成绩段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]的人数进行了统计,丙得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com