
分析 a1=1,an+1=$\left\{\begin{array}{l}{{a}_{n}+3,\frac{n}{3}∉{N}^{*}}\\{{a}_{n},\frac{n}{3}∈{N}^{*}}\end{array}\right.$,可得:a3n-1=a3n-2+3,a3n=a3n-1+3,可得a3n-2+a3n-1+a3n=3a3n-2+9.a3n+1=a3n=a3n-1+3=a3n-2+6,又a1=1,可得a3n-2=1+6(n-1)=6n-5.即可得出S3n=(a1+a2+a3)+…+(a3n-2+a3n-1+a3n)=9n2+3n.S3n≤λ•3n-1,即9n2+3n≤λ•3n-1,λ≥$\{\frac{9{n}^{2}+3n}{{3}^{n-1}}{\}}_{max}$.通过作差可得其单调性,即可得出最大值.
解答 解:∵a1=1,an+1=$\left\{\begin{array}{l}{{a}_{n}+3,\frac{n}{3}∉{N}^{*}}\\{{a}_{n},\frac{n}{3}∈{N}^{*}}\end{array}\right.$,
可得:a3n-1=a3n-2+3,a3n=a3n-1+3,可得a3n-2+a3n-1+a3n=3a3n-2+9.
a3n+1=a3n=a3n-1+3=a3n-2+6,又a1=1,
∴a3n-2=1+6(n-1)=6n-5.
∴S3n=(a1+a2+a3)+…+(a3n-2+a3n-1+a3n)
=3(a1+a4+…+a3n-2)+9n
=3×$\frac{n(1+6n-5)}{2}$+9n
=9n2+3n.
S3n≤λ•3n-1,即9n2+3n≤λ•3n-1,∴λ≥$\{\frac{9{n}^{2}+3n}{{3}^{n-1}}{\}}_{max}$.
设$\frac{9{n}^{2}+3n}{{3}^{n-1}}$=cn,则cn+1-cn=$\frac{9(n+1)^{2}+3(n+1)}{{3}^{n}}$-$\frac{9{n}^{2}+3n}{{3}^{n-1}}$=$\frac{-2(3{n}^{2}-2n-2)}{{3}^{n-1}}$.
当n=1时,3n2-2n-2<0,即c1<c2;
当n≥2时,3n2-2n-2>0,可得:c2>c3>c4>…>cn.
因此(cn)max=c2=14.
∴λ≥14.
故答案为:[14,+∞).
点评 本题考查了等差数列的通项公式、数列递推关系、分类讨论方法、数列的单调性、作差法,考查了推理能力与计算能力,属于难题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:选择题
| 使用年数x(单位:年) | 1 | 2 | 3 | 4 | 5 |
| 维修总费用y(单位:万元) | 0.5 | 1.2 | 2.2 | 3.3 | 4.5 |
| A. | 8年 | B. | 9年 | C. | 10年 | D. | 11年 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,使得sinx+cosx=$\frac{3}{2}$ | B. | ?x0∈R,使得$x_0^2-{x_0}+1=0$ | ||
| C. | ?x∈(0,+∞),ex>x+1 | D. | ?x∈(0,π),sinx>cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值为1 | B. | 图象关于直线x=-$\frac{π}{2}$对称 | ||
| C. | 既是奇函数又是周期函数 | D. | 图象关于点($\frac{3π}{4}$,0)中心对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
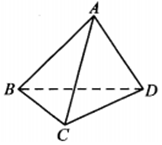 在四面体ABCD中,二面角A-BC-D为60°,点P为直线BC上一动点,记直线PA与平面BCD所成的角为θ,则( )
在四面体ABCD中,二面角A-BC-D为60°,点P为直线BC上一动点,记直线PA与平面BCD所成的角为θ,则( )| A. | θ的最大值为60° | B. | θ的最小值为60° | C. | θ的最大值为30° | D. | θ的最小值为30° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com