
分析 连结A1B、A1D,在平面A1BC上作BE⊥A1C,垂足E,根据二面角平面角的定义证明BEO是二面角B-A1C-A的平面角,根据三角形的边角关系进行求解即可.
解答 解:连结A1B、A1D,在平面A1BC上作BE⊥A1C,垂足E,连结DE,BD,AC,AC和BD交于O,连EO,
∵BC⊥平面ABB1A1,
A1B?平面ABB1A1,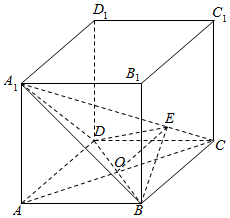
∴BC⊥A1B,
△A1BC是Rt△,同理△A1DC也是Rt△,
则Rt△A1BC≌Rt△A1DC,
则DE⊥A1C,
即连接OE,则∠BEO是二面角B-A1C-A的平面角,
设棱长为1,A1B=$\sqrt{2}$,A1C=$\sqrt{3}$,
△A1BC的面积S=$\frac{1}{2}$BE•A1C=$\frac{1}{2}$A1B•BC,
BE=$\frac{\sqrt{6}}{3}$,
则DE=BE=$\frac{\sqrt{6}}{3}$,BD=$\sqrt{2}$,
BO=$\frac{\sqrt{2}}{2}$,
在△BEO中,
sin∠OEB=$\frac{OB}{BE}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{6}}{3}}$=$\frac{\sqrt{3}}{2}$,
则∠OEB=60°,
∴二面角B-A1C-A的大小为60°.
故答案为:60°
点评 本题主要考查二面角的求解,根据二面角的定义求出二面角的平面角是解决本题的关键.考查学生的推理能力,本题也可以建立坐标系,利用向量法进行求解.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
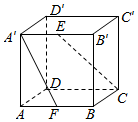 如图,在棱长为2的正方体ABCD-A′B′C′D′中,E、F分别是A′B′和AB的中点.求:
如图,在棱长为2的正方体ABCD-A′B′C′D′中,E、F分别是A′B′和AB的中点.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,AB是圆O的直径,BC与圆O相切于B,D为圆O上一点,∠ADC+∠DCO=180°.
如图所示,AB是圆O的直径,BC与圆O相切于B,D为圆O上一点,∠ADC+∠DCO=180°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,圆内接四边形ABCD中,BD是圆的直径,AB=AC,延长AD与BC的延长线相交于点E,作EF⊥BD于F.
如图,圆内接四边形ABCD中,BD是圆的直径,AB=AC,延长AD与BC的延长线相交于点E,作EF⊥BD于F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
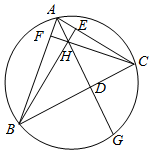 如图,已知AD、BE、CF分别是△ABC三边的高,H是垂心,AD的延长线交△ABC的外接圆于点G.
如图,已知AD、BE、CF分别是△ABC三边的高,H是垂心,AD的延长线交△ABC的外接圆于点G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组号 | 分组 | 回答 正确 的人数 | 回答正确 的人数占本 组的频率 | 频率正确直方图 |
| 第1组 | [15,25) | 5 | 0.5 | 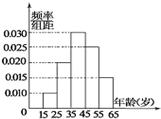 |
| 第2组 | [25,35) | a | 0.9 | |
| 第3组 | [35,45) | 27 | x | |
| 第4组 | [45,55) | 9 | 0.36 | |
| 第5组 | [55,65) | 3 | 0.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com