
分析 (Ⅰ)由矩阵A求得丨A丨和其伴随矩阵A*,由A-1=$\frac{1}{丨A丨}$•A*,即可求得逆矩阵A-1;
(Ⅱ) 将二元一次方程组转化成$A({\begin{array}{l}x\\ y\end{array}})=({\begin{array}{l}2\\ 3\end{array}})$,由(Ⅰ)可知$(\begin{array}{l}{x}\\{y}\end{array})$=A-1$(\begin{array}{l}{2}\\{3}\end{array})$,即可求得方程组的解.
解答 解:(Ⅰ)丨A丨=3×2-4×1=2,
A的伴随矩阵A*=$[\begin{array}{l}{2}&{-1}\\{-4}&{3}\end{array}]$,
由A-1=$\frac{1}{丨A丨}$•A*=$[\begin{array}{l}{1}&{-\frac{1}{2}}\\{-2}&{\frac{3}{2}}\end{array}]$,
∴${A^{-1}}=({\begin{array}{l}1&{-\frac{1}{2}}\\{-2}&{\frac{3}{2}}\end{array}})$…(3分)
(Ⅱ) 方程组可写为$A({\begin{array}{l}x\\ y\end{array}})=({\begin{array}{l}2\\ 3\end{array}})$,(4分)
因此原方程组的解:$(\begin{array}{l}{x}\\{y}\end{array})$=A-1$(\begin{array}{l}{2}\\{3}\end{array})$=$(\begin{array}{l}{1}&{-\frac{1}{2}}\\{-2}&{\frac{3}{2}}\end{array})$$(\begin{array}{l}{2}\\{3}\end{array})$=$(\begin{array}{l}{\frac{1}{2}}\\{\frac{1}{2}}\end{array})$,
∴方程组的解为:$\left\{\begin{array}{l}x=\frac{1}{2}\\ y=\frac{1}{2}\end{array}\right.$.(7分)
点评 本题考查逆变换与逆矩阵的应用,考查求二阶矩阵的逆矩阵,系数矩阵的逆矩阵解方程组等基础知识,考查运算求解能力与转化思想.属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{8}$ | D. | -$\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
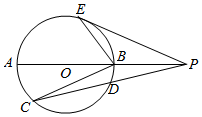 如图,半径为2的⊙O的直径AB的延长线与弦CD的延长线相交与点P,PE为⊙O的切线,E为切点,$\overrightarrow{BE}$=2$\overrightarrow{BD}$,若PB=2,PD=$\frac{5}{2}$,∠PEB=30°.
如图,半径为2的⊙O的直径AB的延长线与弦CD的延长线相交与点P,PE为⊙O的切线,E为切点,$\overrightarrow{BE}$=2$\overrightarrow{BD}$,若PB=2,PD=$\frac{5}{2}$,∠PEB=30°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数y=f(x)在区间[a,b]的图象如图所示,则其导函数y=f′(x)在该区间( )
已知函数y=f(x)在区间[a,b]的图象如图所示,则其导函数y=f′(x)在该区间( )| A. | 先递减再递增 | B. | 先递增再递减 | ||
| C. | 先递增再递减最后又递增 | D. | 先递减再递增最后又递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com