
分析 (I)设“父母二人所得红包金额分别在(0,50]和(100,200]”为事件A,由此利用等可能事件概率计算公式父母二人所得红包金额分别在(50,100]和(100,200]的概率.
(II)由题意随机变量X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(I)设“父母二人所得红包金额分别在(0,50]和(100,200]”为事件A,
则 $P(A)=\frac{C_3^1C_3^1A_2^2}{{A_{10}^2}}=\frac{1}{5}$.
(II)(7分)由题意,X=0,1,2,3,
$P(X=0)=\frac{C_6^3}{{C_{10}^3}}=\frac{1}{6}$,
$P(X=1)=\frac{C_4^1C_6^2}{{C_{10}^3}}=\frac{1}{2}$,
$P(X=2)=\frac{C_4^2C_6^1}{{C_{10}^3}}=\frac{3}{10}$,
$P(X=3)=\frac{C_4^3}{{C_{10}^3}}=\frac{1}{30}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{6}$ | $\frac{1}{2}$ | $\frac{3}{10}$ | $\frac{1}{30}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


科目:高中数学 来源: 题型:解答题
 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良101-150为轻度污染;151-200为中度污染;201~300为重度污染;>300为严重污染.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良101-150为轻度污染;151-200为中度污染;201~300为重度污染;>300为严重污染.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 水是最常见的物质之一,是包括人类在内所有生命生存的重要资源,也是生物体最重要的组成部分.为了推动对水资源进行综合性统筹规划和管理,加强水资源保护,解决日益严峻的淡水缺乏问题,开展广泛的宣传以提高公众对开发和保护水资源的认识.中国水利部确定每年的3月22日至28日为“中国水周”,以提倡市民节约用水.某市统计局调查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如图所示.将月用水量落入各组的频率视为概率,并假设每天的用水量相互独立.
水是最常见的物质之一,是包括人类在内所有生命生存的重要资源,也是生物体最重要的组成部分.为了推动对水资源进行综合性统筹规划和管理,加强水资源保护,解决日益严峻的淡水缺乏问题,开展广泛的宣传以提高公众对开发和保护水资源的认识.中国水利部确定每年的3月22日至28日为“中国水周”,以提倡市民节约用水.某市统计局调查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如图所示.将月用水量落入各组的频率视为概率,并假设每天的用水量相互独立.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
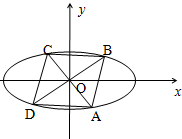 已知M(-2$\sqrt{2}$,0),N(2$\sqrt{2}$,0)为椭圆的左、右顶点,P是椭圆上异于M,N的动点,且△PMN的面积最大值为4$\sqrt{2}$.
已知M(-2$\sqrt{2}$,0),N(2$\sqrt{2}$,0)为椭圆的左、右顶点,P是椭圆上异于M,N的动点,且△PMN的面积最大值为4$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1009 | B. | 1010 | C. | 1009,1010 | D. | 2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,扇形OAB的中心角为直角,半径为1,点P为扇形OAB的弧$\widehat{AB}$上任意一点,设$\overrightarrow{OP}$=x$\overrightarrow{OB}$+y$\overrightarrow{OA}$(x,y∈R),$\overrightarrow a$=(x,y),$\overrightarrow b$=(${\sqrt{3}$,1),则$\overrightarrow a•\overrightarrow b$的最小值为( )
如图,扇形OAB的中心角为直角,半径为1,点P为扇形OAB的弧$\widehat{AB}$上任意一点,设$\overrightarrow{OP}$=x$\overrightarrow{OB}$+y$\overrightarrow{OA}$(x,y∈R),$\overrightarrow a$=(x,y),$\overrightarrow b$=(${\sqrt{3}$,1),则$\overrightarrow a•\overrightarrow b$的最小值为( )| A. | -1 | B. | -2 | C. | 1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 售价(单位:元) | 23 | 21 | 20 |
| 日销量(单位:个) | 10 | 15 | 20 |
| 频数 | 4 | 14 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com