
 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良101-150为轻度污染;151-200为中度污染;201~300为重度污染;>300为严重污染.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良101-150为轻度污染;151-200为中度污染;201~300为重度污染;>300为严重污染.分析 (1)从茎叶图中可以发现这样本中空气质量优的天数为2,空气质量良的天数为4,由此能求出该样本中空气质量优良的频率,从而能估计该月空气质量优良的天数.
(2)估计某天空气质量优良的概率为$\frac{3}{5}$,ξ的所有可能取值为0,1,2,3,且ξ~B(3,$\frac{3}{5}$),由此能求出ξ的概率分布列和数学期望.
解答 解:(1)从茎叶图中可以发现这样本中空气质量优的天数为2,
空气质量良的天数为4,
∴该样本中空气质量优良的频率为$\frac{6}{10}=\frac{3}{5}$,
从而估计该月空气质量优良的天数为30×$\frac{3}{5}$=18.
(2)由(1)估计某天空气质量优良的概率为$\frac{3}{5}$,ξ的所有可能取值为0,1,2,3,
且ξ~B(3,$\frac{3}{5}$),
P(ξ=0)=($\frac{2}{5}$)3=$\frac{8}{125}$,
P(ξ=1)=${C}_{3}^{1}(\frac{3}{5})(\frac{2}{5})^{2}$=$\frac{36}{125}$,
P(ξ=2)=${C}_{3}^{2}(\frac{3}{5})^{2}(\frac{2}{5})$=$\frac{54}{125}$,
P(ξ=3)=($\frac{3}{5}$)3=$\frac{27}{125}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{8}{125}$ | $\frac{36}{125}$ | $\frac{54}{125}$ | $\frac{27}{125}$ |
点评 本题考查茎叶图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


科目:高中数学 来源: 题型:解答题
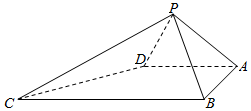 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .2或-1 | B. | .2 | C. | -1 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 52 | 5149 | 48 | 53 | 48 | 49 |
| 乙 | 60 | 6540 | 35 | 25 | 65 | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com