
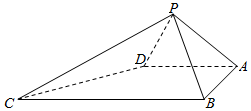
 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.分析 (1)取BC的中点E,连接DE,过P作PO⊥平面ABCD,垂足为O,连接OA,OB,OE,OD,推出OE⊥PB,证明OE∥CD,得到PB⊥CD.
(2)由OE,OB,OP两两垂直.以O为原点,OE方向为x轴正方向,OB方向为y轴正方向,OP方向为z轴正方向,
建立空间直角坐标系O-xyz,求出相关点的坐标,求出平面PAD的法向量,平面PBD的法向量为$\overrightarrow m$,利用空间向量的数量积求解即可.
解答  解:(1)证明:取BC的中点E,连接DE,则ADEB为正方形,
解:(1)证明:取BC的中点E,连接DE,则ADEB为正方形,
过P作PO⊥平面ABCD,垂足为O,
连接OA,OB,OE,OD,…(2分)
由△PAB和△PAD都是等边三角形可知PA=PB=PD,
所以OA=OB=OD,
即点O为正方形ADEB对角线的交点…(4分)
故OE⊥BD,从而OE⊥平面PBD,所以OE⊥PB,
因为O是BD的中点,E是BC的中点,
所以OE∥CD,因此PB⊥CD…(6分)
(2)由(1)可知,OE,OB,OP两两垂直.
以O为原点,OE方向为x轴正方向,OB方向为y轴正方向,OP方向为z轴正方向,
建立如图所示的直角坐标系O-xyz,…(7分)
设|AB|=2,则$A(-\sqrt{2},0,0)$,$D(0,-\sqrt{2},0)$,$P(0,0,\sqrt{2})$,$\overrightarrow{AD}=(\sqrt{2},-\sqrt{2},0)$,$\overrightarrow{AP}=(\sqrt{2},0,\sqrt{2})$,…(8分)
设平面PAD的法向量$\overrightarrow n=(x,y,z)$,$\overrightarrow n•\overrightarrow{AD}=\sqrt{2}x-\sqrt{2}y=0$,$\overrightarrow n•\overrightarrow{AP}=\sqrt{2}x+\sqrt{2}z=0$,
取x=1,得y=1,z=-1,即$\overrightarrow n=(1,1,-1)$,…(10分)
因为OE⊥平面PBD,设平面PBD的法向量为$\overrightarrow m$,取$\overrightarrow m=(1,0,0)$,
由图象可知二面角A-PD-B的大小为锐角,…(11分)
所以二面角A-PD-B的余弦值为$cosθ=\frac{{|{\overrightarrow n•\overrightarrow m}|}}{{|{\overrightarrow n}|•|{\overrightarrow m}|}}=\frac{1}{{\sqrt{3}}}=\frac{{\sqrt{3}}}{3}$…(12分)
点评 本题考查直线与直线的垂直,直线与平面垂直的想知道了的应用,空间向量的数量积的应用,考查计算能力.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2) | B. | (-2,+∞) | C. | (-∞,0) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
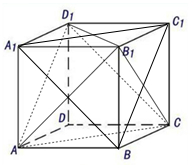 正方体ABCD-A1B1C1D1中,连接A1C1,A1B,BC1,AD1,AC,CD1.
正方体ABCD-A1B1C1D1中,连接A1C1,A1B,BC1,AD1,AC,CD1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良101-150为轻度污染;151-200为中度污染;201~300为重度污染;>300为严重污染.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良101-150为轻度污染;151-200为中度污染;201~300为重度污染;>300为严重污染.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 水是最常见的物质之一,是包括人类在内所有生命生存的重要资源,也是生物体最重要的组成部分.为了推动对水资源进行综合性统筹规划和管理,加强水资源保护,解决日益严峻的淡水缺乏问题,开展广泛的宣传以提高公众对开发和保护水资源的认识.中国水利部确定每年的3月22日至28日为“中国水周”,以提倡市民节约用水.某市统计局调查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如图所示.将月用水量落入各组的频率视为概率,并假设每天的用水量相互独立.
水是最常见的物质之一,是包括人类在内所有生命生存的重要资源,也是生物体最重要的组成部分.为了推动对水资源进行综合性统筹规划和管理,加强水资源保护,解决日益严峻的淡水缺乏问题,开展广泛的宣传以提高公众对开发和保护水资源的认识.中国水利部确定每年的3月22日至28日为“中国水周”,以提倡市民节约用水.某市统计局调查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如图所示.将月用水量落入各组的频率视为概率,并假设每天的用水量相互独立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com