
| A. | (-∞,-2) | B. | (-2,+∞) | C. | (-∞,0) | D. | (0,+∞) |
分析 由题意知a3-2a>m+a,a≥0,从而可得m<a3-3a在[0,+∞)上恒成立,令f(x)=x3-3x,求导判断函数的单调性并求最值即可.
解答 解:∵复数z=a3-2a+(m+a)i(a≥0,m∈R)的实部大于虚部,
∴a3-2a>m+a,a≥0,
即m<a3-3a在[0,+∞)上恒成立,
令f(x)=x3-3x,故f′(x)=3x2-3=3(x+1)(x-1),
故f(x)在[0,1)上是减函数,在[1,+∞)上是增函数,
故fmin(x)=f(1)=1-3=-2,
故m<-2,
故选:A.
点评 本题考查了导数的综合应用及复数的应用,同时考查了函数思想与转化思想的应用,属于中档题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{2}})$ | B. | $[{\frac{1}{2},1}]$ | C. | $({0,\frac{1}{2}}]∪[{1,+∞})$ | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
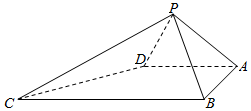 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com