
分析 (1)根据动圆过定点以及直线和x轴相交的弦长理由参数消元法即可求动圆圆心的轨迹E的方程;
(2)设A(x1,y1),B(x2,y2),x1≠x2,P(x0,y0),利用设而不求的思想,结合曲线在A,B处的切线方程,求出交点坐标借助向量数量积的关系进行转化求解即可.
解答 解:(1)设动圆圆心的坐标为(x,y),半径r,(r>0),
∵动圆过定点R(0,2),且在x轴上截得线段MN的长为4,
∴$\left\{\begin{array}{l}{{x}^{2}+(y-2)^{2}={r}^{2}}\\{{y}^{2}+4={r}^{2}}\end{array}\right.$,消去r得x2=4y,
故所求轨迹E的方程为x2=4y;
(2)实数t是定值,且t=1,下面说明理由,
不妨设A(x1,y1),B(x2,y2),x1≠x2,
P(x0,y0),由题知Q(0,1),
由$\left\{\begin{array}{l}{y=kx+t}\\{{x}^{2}=4y}\end{array}\right.$,消去y得x2-4kx-4t=0,
∴$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=4k}\\{{x}_{1}{x}_{2}=-4t}\end{array}\right.$,轨迹E在A点处的切线方程为l1:y-y1=$\frac{{x}_{1}}{2}$(x-x1),即y=$\frac{{x}_{1}}{2}$x-$\frac{{{x}_{1}}^{2}}{4}$,
同理,轨迹E在B处的切线方程为l1:y=$\frac{{x}_{2}}{2}$x-$\frac{{{x}_{2}}^{2}}{4}$,
联立l1,l2:的方程解得交点坐标P($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{x}_{1}{x}_{2}}{4}$),即P(2k,-t),
由|$\overrightarrow{PA}$|•|$\overrightarrow{PB}$|sin∠APB=|$\overrightarrow{PQ}$|•|$\overrightarrow{AB}$|=2S△APB,
得$\overrightarrow{PQ}$⊥$\overrightarrow{AB}$,即$\overrightarrow{PQ}$•$\overrightarrow{AB}$=0,
$\overrightarrow{PQ}$=(-2k,2t),$\overrightarrow{AB}$=(x2-x1,$\frac{{{x}_{2}}^{2}-{{x}_{1}}^{2}}{4}$),
∴-2k(x2-x1)+2t•$\frac{{{x}_{2}}^{2}-{{x}_{1}}^{2}}{4}$=0,
即2k(x2-x1)(t-1)=0,
则2k(t-1)=0,
则t=1,
故实数t是定值,且t=1.
点评 本题主要考查与圆有关的轨迹问题,涉及直线和抛物线的相交的位置关系,利用设而不求的数学思想是解决本题的关键.综合性较强,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{2}})$ | B. | $[{\frac{1}{2},1}]$ | C. | $({0,\frac{1}{2}}]∪[{1,+∞})$ | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
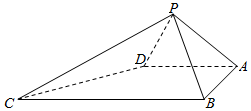 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .2或-1 | B. | .2 | C. | -1 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,BC∥AD,PA⊥AD,平面PAB⊥平面ABCD,∠BAD=120°,且PA=AB=BC=$\frac{1}{2}$AD=2.
在四棱锥P-ABCD中,BC∥AD,PA⊥AD,平面PAB⊥平面ABCD,∠BAD=120°,且PA=AB=BC=$\frac{1}{2}$AD=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com