
分析 利用数量积运算、投影的意义即可得出.
解答 解:∵|${\overrightarrow a}$|=2,$\overrightarrow e$为单位向量,
∴($\overrightarrow a$+$\overrightarrow e$)•($\overrightarrow a$-$\overrightarrow e$)=$\overrightarrow a$2-$\overrightarrow e$2=4-1=3,
∴|$\overrightarrow a$-$\overrightarrow e$|2=$\overrightarrow a$2+$\overrightarrow e$2-2$\overrightarrow a$•$\overrightarrow e$=$\overrightarrow a$2+$\overrightarrow e$2-2|$\overrightarrow a$|•|$\overrightarrow e$|cos$\frac{π}{3}$=4+1-2×2×1×$\frac{1}{2}$=3,
∴|$\overrightarrow a$-$\overrightarrow e$|=$\sqrt{3}$,
∴$\overrightarrow a$+$\overrightarrow e$在$\overrightarrow a$-$\overrightarrow e$上的投影为$\frac{(\overrightarrow{a}+\overrightarrow{e})•(\overrightarrow{a}-\overrightarrow{e})}{|\overrightarrow{a}-\overrightarrow{e}|}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$
故答案为:$\sqrt{3}$
点评 本题考查了数量积运算、投影的意义,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∧(¬q) | C. | (¬p)∧q | D. | p∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
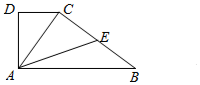 如图,在直角梯形ABCD中,AB∥CD,∠ADC=90°,AB=3,AD=$\sqrt{2}$,E为BC中点,若$\overrightarrow{AB}$•$\overrightarrow{AC}$=3,则$\overrightarrow{AE}$•$\overrightarrow{BC}$=-3.
如图,在直角梯形ABCD中,AB∥CD,∠ADC=90°,AB=3,AD=$\sqrt{2}$,E为BC中点,若$\overrightarrow{AB}$•$\overrightarrow{AC}$=3,则$\overrightarrow{AE}$•$\overrightarrow{BC}$=-3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com