
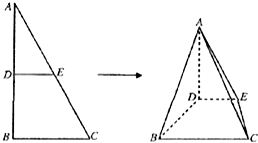
 如图,△ABC中,AB=2,BC=1,∠ABC=90°,D,E分别为AB,AC上的点,DE∥BC,将△ADE沿DE折到△A′DE的位置,使平面A′DE⊥平面BCED.
如图,△ABC中,AB=2,BC=1,∠ABC=90°,D,E分别为AB,AC上的点,DE∥BC,将△ADE沿DE折到△A′DE的位置,使平面A′DE⊥平面BCED.| π |
| 2 |
| ||
| 2 |
| 2 |
| CF |
| A′F |
| ||
| 2 |
| π |
| 4 |
1+
| ||||
1-
|
| 2 |
| x |
| 2 |
| 1 |
| 3 |
(
| ||
| 2 |
| 4x-x3 |
| 12 |
| 4-3x2 |
| 12 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
4
| ||
| 27 |


科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 从某批苹果中随机抽取100个苹果进行重量(单位:克)调查.发现重量都在70克至100克之间,结果如表:
从某批苹果中随机抽取100个苹果进行重量(单位:克)调查.发现重量都在70克至100克之间,结果如表:| 分数(重量) | [70,75) | [75,80) | [80,85) | [85,90) | [90,95) | [95,100) |
| 频数(个) | 5 | 10 | 20 | 30 | x | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| an•an+1 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com