

分析 (1)作出BD在α内的射影,根据勾股定理求出D到平面α的距离,即可求出线面角的大小;
(2)使用$\overrightarrow{AC},\overrightarrow{BD}$表示出$\overrightarrow{MN}$,即可证明$\overrightarrow{MN}$与$\overrightarrow{AC}$,$\overrightarrow{BD}$共面;
(3)对(2)中的结论两边平方,得出MN的长度表达式,根据θ的范围求出MN的最大值.
解答 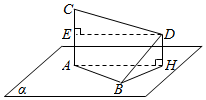 解:(1)设D在α上的射影为H,∵AC⊥α,DH⊥α,∴AC∥DH,∴AC,DH共面,
解:(1)设D在α上的射影为H,∵AC⊥α,DH⊥α,∴AC∥DH,∴AC,DH共面,
∴过D作DK⊥AC于K,则AHDK为矩形,∴DK=AH.
设DH=h,则(AC-h)2+AH2=CD2,①
∵BD⊥AB,AB⊥DH,∴BH⊥AB,
∴AH2=AB2+BH2=AB2+(BD2-h2)②
将②代入①,得:(24-h)2+72+(242-h2)=252,解得h=12,
于是$sin∠DBH=\frac{1}{2}$,∴∠DBH=30°,即BD与α所成的是30°.
(2)解:∵$\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AC}+\overrightarrow{CN}$,$\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BD}+\overrightarrow{DN}$,
∴2$\overrightarrow{MN}$=$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{CN}+\overrightarrow{DN}+\overrightarrow{AC}+\overrightarrow{BD}$=$\overrightarrow{AC}+\overrightarrow{BD}$.
∴$\overrightarrow{MN},\overrightarrow{AC},\overrightarrow{BD}$共面.
∴一定存在一个过MN的平面与AC,BD同时平行.
(3)由(2)得$\overrightarrow{MN}$=$\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{BD}$,
∴${\overrightarrow{MN}}^{2}$=$\frac{1}{4}{\overrightarrow{AC}}^{2}$+$\frac{1}{4}{\overrightarrow{BD}}^{2}$+$\frac{1}{2}$$\overrightarrow{AC}•\overrightarrow{BD}$=$\frac{1}{4}×2{4}^{2}$+$\frac{1}{4}×2{4}^{2}$+$\frac{1}{2}×24×24$cos($\frac{π}{2}-θ$)=288(1+sinθ).
∴MN=$\sqrt{288(1+sinθ)}$=12$\sqrt{2+2sinθ}$.(θ∈[0,$\frac{π}{2}$)).
∴12$\sqrt{2}$≤MN<24.
∴当MN大于或大于24米时一定够用.
点评 本题考查了线面垂直的性质,直线共面的判断,向量法在几何中的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{5}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | 不存在最大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}-1$ | B. | $\sqrt{3}-1$ | C. | $2-\sqrt{2}$ | D. | $3-\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-2y-6=0 | B. | 2x-3y+6=0 | C. | 2x-3y-6=0 | D. | 3x-2y+6=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\overrightarrow i+\overrightarrow j$ | B. | $2\overrightarrow i-\overrightarrow j$ | C. | $\overrightarrow i-2\overrightarrow j$ | D. | $\overrightarrow i+2\overrightarrow j$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既奇又偶函数 | B. | 偶函数 | C. | 非奇非偶函数 | D. | 奇函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com