
分析 用分层抽样的方法抽取一个容量为45的样本,根据高一年级抽20人,高三年级抽10人,得到高二年级要抽取的人数,根据该高级中学共有900名学生,算出高二年级学生人数.
解答 解:∵用分层抽样的方法从某校学生中抽取一个容量为45的样本,
其中高一年级抽20人,高三年级抽10人,
∴高二年级要抽取45-20-10=15,
∵高级中学共有900名学生,
∴每个个体被抽到的概率是$\frac{45}{900}$=$\frac{1}{20}$
∴该校高二年级学生人数为$\frac{15}{\frac{1}{20}}$=300,
故答案为:300.
点评 本题考查分层抽样,抽样过程中每个个体被抽到的可能性相同,这是解决抽样问题的依据,样本容量、总体个数、每个个体被抽到的概率,这三者可以做到知二求一.


科目:高中数学 来源: 题型:解答题
 如图,已知菱形ABCD的边长为6,∠BAD=60°,AC∩BD=0,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点.
如图,已知菱形ABCD的边长为6,∠BAD=60°,AC∩BD=0,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
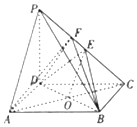 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为矩形,E为PC的中点,且$PD=AD=\frac{1}{2}AB=4$.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为矩形,E为PC的中点,且$PD=AD=\frac{1}{2}AB=4$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com