
分析 (I)求出函数的定义域,红丝带导数,求出极值点,利用函数的单调性求解a的范围.
(II)由(I)知,求出f(x)min时的a值,利用条件当x≥0时f(x)≤kx2,转化为当x≥0时,x-ln(x+1)≤kx2成立,当k≤0时,当k>0时,分别判断求解.(1)当$k≥\frac{1}{2}$时,(2)当$0<k<\frac{1}{2}$时,利用函数的单调性推出K的范围.
解答 解:(I)函数的定义域为(-a,+∞).$f'(x)=\frac{x+a-1}{x+a}(x>-a)$,…(1分)
由f'(x)=0⇒x=1-a,
因为函数f(x)在(0,+∞)为增函数.
所以1-a≤0,从而a≥1…(4分)
(II)由(I)知,函数f(x)在(-a,1-a)为减函数,在(1-a,+∞)为增函数.
所以f(x)min=f(1-a)=1-a=0得a=1…(6分)
所以当x≥0时f(x)≤kx2即是当x≥0时,x-ln(x+1)≤kx2成立
当k≤0时,因为f(1)=1-ln2>0所以k≤0不合题意…(7分)
当k>0时,令g(x)=f(x)-kx2=x-ln(x+1)-kx2(x≥0)$g'(x)=\frac{-x[2kx-(1-2k)]}{x+1}$,
令g'(x)=0得${x_1}=0,{x_2}=\frac{1}{2k}-1>-1$…(8分)
(1)当$k≥\frac{1}{2}$时,g(x)在(0,+∞)单调递减,
于是g(x)≤g(0)=0成立.所以$k≥\frac{1}{2}$适合题意…(10分)
(2)当$0<k<\frac{1}{2}$时,g(x)在$(0,\frac{1}{2k}-1)$单调递增,
所以当$x∈(0,\frac{1}{2k}-1)$时,g(x)>g(0)=0,
故$0<k<\frac{1}{2}$不合题意.综上:$k≥\frac{1}{2}$…(12分)
点评 本题考查函数的导数的综合应用,函数的极值以及函数的单调性的应用,考查分类讨论以及转化思想的应用.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1或3 | B. | 3 | C. | 27 | D. | -1或27 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线m,n和平面α成等角 | B. | m⊥α且n⊥α | ||
| C. | m∥α且n?α | D. | m∥α且n∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
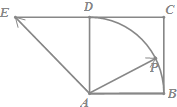 如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ的最小值为( )
如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ的最小值为( )| A. | $\sqrt{5}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
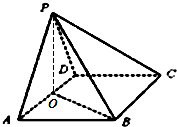 如图,在四棱锥P-ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com