
分析 通过化简可得$\frac{1}{4}$sinα+$\frac{3}{4}$cosα=0,进而可得tanα的值.
解答 解:∵$\overrightarrow a$=($\frac{3}{4}$,sinα),$\overrightarrow b$=(cosα,$\frac{1}{4}$)且$\overrightarrow{a}$⊥$\overrightarrow{b}$,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=($\frac{3}{4}$,sinα)•(cosα,$\frac{1}{4}$)=$\frac{1}{4}$sinα+$\frac{3}{4}$cosα=0,
∴$\frac{sinα}{cosα}$=$\frac{3}{1}$,即tanα=-3,
故答案为:-3.
点评 本题考查平面向量数量积的运算,注意解题方法的积累,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
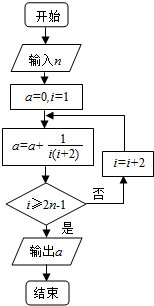
| A. | $\frac{2015}{4031}$ | B. | $\frac{4030}{4031}$ | C. | $\frac{2014}{4029}$ | D. | $\frac{2015}{4029}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
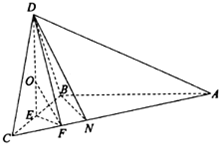
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
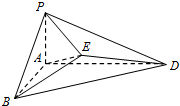
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com