
分析 (1)观察向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$的系数,分析不存在不存在常数λ使$\overrightarrow{a}=λ\overrightarrow{b}$成立;
(2)求出$\overrightarrow{BD}$,观察与$\overrightarrow{AB}$的关系.
解答 解:(1)因为已知向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$两个不共线,并且$\overrightarrow{a}$=3$\overrightarrow{{e}_{1}}$+4$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=6$\overrightarrow{{e}_{1}}$-8$\overrightarrow{{e}_{2}}$,所以不存在常数λ使$\overrightarrow{a}=λ\overrightarrow{b}$,所以$\overrightarrow{a}$、$\overrightarrow{b}$不共线;
(2)证明:
因为$\overrightarrow{AB}$=2$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$,$\overrightarrow{BC}$=6$\overrightarrow{{e}_{1}}$+23$\overrightarrow{{e}_{2}}$,$\overrightarrow{CD}$=4($\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$),所以$\overrightarrow{BD}=\overrightarrow{BC}+\overrightarrow{CD}$=$10\overrightarrow{{e}_{1}}+15\overrightarrow{{e}_{2}}=5(2\overrightarrow{{e}_{1}}+3\overrightarrow{{e}_{2}})=5\overrightarrow{AB}$,
所以$\overrightarrow{AB},\overrightarrow{BD}$共线,又有公共点B,所以A、B、D三点共线.
点评 本题考查了平面向量共线基本道理的运用;利用向量证明三点共线,只要证明向量共线并且有公共点即可.


科目:高中数学 来源: 题型:选择题
| A. | -1或3 | B. | 3 | C. | 27 | D. | -1或27 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
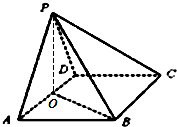 如图,在四棱锥P-ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com