
分析 (1)由P在圆上,且$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,可知直线l过圆心O,由此求出b的值;
(2)由|AB|=2$\sqrt{3}$得到原点O到直线l的距离,再由面积为$\frac{2\sqrt{3}}{3}$得另一关于k和b的等式,联立方程组求得满足条件的k值;
(3)联立直线方程和圆的方程,化为关于x的一元二次方程,由|PA|•|PB|=4得到A,B两点横坐标的关系,结合根与系数的关系得到直线l的斜率和截距的关系,由点到直线的距离公式求出P到直线l的距离为定值,由此可得存在一定圆M,方程是x2+(y-2)2=1,使得直线l与圆M相切.
解答 解:(Ⅰ)∵点P(0,2)在圆C:x2+y2=4上,且直线l:y=kx+b与圆C交于A,B两点,
当$\overrightarrow{PA}$•$\overrightarrow{PB}$=0时,$\overrightarrow{PA}⊥\overrightarrow{PB}$,
∴直线l过圆心O(0,0),则b=0;
(Ⅱ)由题意可知,直线l不过原点O,不妨设k>0,b>0,
由|AB|=2$\sqrt{3}$,得$\frac{|b|}{\sqrt{{k}^{2}+1}}=\sqrt{4-(\sqrt{3})^{2}}=1$,①
取x=0,得y=b,取y=0,得x=-$\frac{b}{k}$,
∴$\frac{1}{2}•\frac{b}{k}•b=\frac{2\sqrt{3}}{3}$,②
联立①②解得:$k=\sqrt{3}$或k=$\frac{\sqrt{3}}{3}$,
由对称性可得满足条件的直线l的斜率的值为$±\frac{\sqrt{3}}{3}$或$±\sqrt{3}$;
(Ⅲ)联立$\left\{\begin{array}{l}{y=kx+b}\\{{x}^{2}+{y}^{2}=4}\end{array}\right.$,消去y,得(k2+1)x2+2kbx+b2-4=0.
设A(x1,y1),B(x2,y2),
∴x1+x2=-$\frac{2kb}{1+{k}^{2}}$,x1x2=$\frac{{b}^{2}-4}{1+{k}^{2}}$,
∵|PA|•|PB|=4,∴$\sqrt{{{x}_{1}}^{2}+({y}_{1}-2)^{2}}•\sqrt{{{x}_{2}}^{2}+({y}_{2}-2)^{2}}=4$,
∴$({{x}_{1}}^{2}+{{y}_{1}}^{2}-4{y}_{1}+4)({{x}_{2}}^{2}+{{y}_{2}}^{2}-4{y}_{2}+4)$=16,
即(2-y1)(2-y2)=1,
∴y1y2-2(y1+y2)+3=0,则(kx1+b)(kx2+b)-2(kx1+b+kx2+b)+3=0,
k2x1x2+(kb-2k)(x1+x2)-4b+3=0,
∴k2•$\frac{{b}^{2}-4}{{k}^{2}+1}$+(kb-2k)•(-$\frac{2kb}{1+{k}^{2}}$)-4b+3=0.
化简得:化简得k2=b2-4b+3,即k2+1=(b-2)2,
∴$\frac{|b-2|}{\sqrt{{k}^{2}+1}}=1$.
∵点P(0,2)到直线l:y=kx+b的距离d=$\frac{|-2+b|}{\sqrt{{k}^{2}+1}}$=1,
∴存在一定圆M,方程是x2+(y-2)2=1,使得直线l与圆M相切.
点评 本题考查了平面向量的应用,考查了直线与圆的位置关系,考查了定值的应用问题,综合性强,属难题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
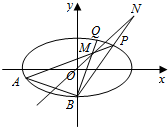 如图,已知椭圆C:$\frac{x^2}{2}$+y2=1,点B坐标为(0,-1),过点B的直线交椭圆C于y轴左侧另外一点A,且线段AB的中点E在直线y=x上.
如图,已知椭圆C:$\frac{x^2}{2}$+y2=1,点B坐标为(0,-1),过点B的直线交椭圆C于y轴左侧另外一点A,且线段AB的中点E在直线y=x上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 参加社团活动 | 不参加社团活动 | 合计 | |
| 学习积极性高 | 17 | 8 | 25 |
| 学习积极性一般 | 5 | 20 | 25 |
| 合计 | 22 | 28 | 50 |
| P(Χ2≥k) | 0.05 | 0.01 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com