
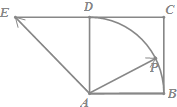
 如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ的最小值为( )
如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ的最小值为( )| A. | $\sqrt{5}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
分析 如图所示,建立直角坐标系.不妨设$\overrightarrow{AB}$=(1,0),$\overrightarrow{AE}$=(-1,1),$\overrightarrow{AP}$=(cosθ,sinθ),利用向量$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,可得λ+μ=2sinθ+cosθ,再利用两角和差的正弦公式及其有界性即可得出.
解答 解:如图所示,建立直角坐标系.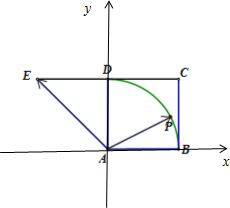
不妨设$\overrightarrow{AB}$=(1,0),$\overrightarrow{AE}$=(-1,1),
$\overrightarrow{AP}$=(cosθ,sinθ),
∵向量$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,
∴(cosθ,sinθ)=λ(1,0)+μ(-1,1)=(λ-μ,μ),
∴$\left\{\begin{array}{l}{λ-μ=cosθ}\\{μ=sinθ}\end{array}\right.$.θ∈[0,$\frac{π}{2}$].
当$\overrightarrow{AP}$=$\overrightarrow{AB}$时,λ=1,μ=0,此时λ+μ取得最小值,最小值是1.
故答案为:1.
点评 本题考查了向量的坐标运算、两角和差的正弦公式及其有界性等基础知识与基本技能方法,考查了推理能力和解决问题的能力,属于中档题.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:解答题
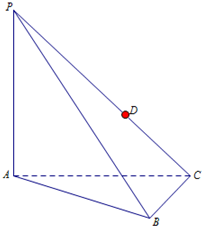 如图,在三棱锥P-ABC中,△ABC为等边三角形,AB=2,AP⊥平面ABC,D为PC上的动点.
如图,在三棱锥P-ABC中,△ABC为等边三角形,AB=2,AP⊥平面ABC,D为PC上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2-$\frac{{x}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{3}$-y2=1 | D. | x2-$\frac{{y}^{2}}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨(¬p) | B. | ¬((¬p)∧(¬p)) | C. | (¬p)∧(¬p) | D. | ¬(p∨p) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
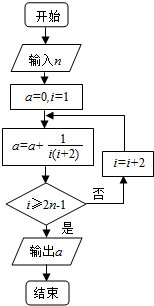
| A. | $\frac{2015}{4031}$ | B. | $\frac{4030}{4031}$ | C. | $\frac{2014}{4029}$ | D. | $\frac{2015}{4029}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com