
分析 (1)对递推式两边取倒数化简即可得出$\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}$=2,结论得证,利用等差数列的通项公式得出$\frac{1}{{a}_{n}}$,再得出an;
(2)使用裂项法求出Sn,使用不等式得出Sn的范围,从而得出k的范围.
解答 (1)证明:∵${a_{n+1}}=\frac{a_n}{{2{a_n}+1}}$,∴$\frac{1}{{{a_{n+1}}}}=\frac{1}{a_n}+2$,
即$\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}$=2,又a1=1,
∴数列$\left\{{\frac{1}{a_n}}\right\}$是以1为首项,2为公差的等差数列,
∴$\frac{1}{a_n}=2n-1$,
∴${a_n}=\frac{1}{2n-1}$.
(2)解:${b_n}=\frac{1}{(2n+1)(2n-1)}=\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴${S_n}=\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})+…+(\frac{1}{2n-1}-\frac{1}{2n+1})]$=$\frac{1}{2}(1-\frac{1}{2n+1})<\frac{1}{2}$,
要使不等式Sn<k对一切n∈N*恒成立,则k$≥\frac{1}{2}$.
∴k的范围为$[{\frac{1}{2},+∞})$.
点评 本题考查了等差数列的判断,等差数列的通项公式,裂项法求和,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {5} | B. | {0,5} | C. | {1,5} | D. | {0,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
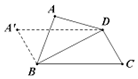 如图,矩形ABCD中,AB=1,BC=$\sqrt{3}$,将△ABD沿对角线BD向上翻折,若翻折过程中AC长度在[$\frac{\sqrt{10}}{2}$,$\frac{\sqrt{13}}{2}$]内变化,则点A所形成的运动轨迹的长度为$\frac{\sqrt{3}π}{12}$.
如图,矩形ABCD中,AB=1,BC=$\sqrt{3}$,将△ABD沿对角线BD向上翻折,若翻折过程中AC长度在[$\frac{\sqrt{10}}{2}$,$\frac{\sqrt{13}}{2}$]内变化,则点A所形成的运动轨迹的长度为$\frac{\sqrt{3}π}{12}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com