Question

20．已知某工厂有25周岁以上（含25周岁）工人300名，25周岁以下工人200名．为研究工人的日平均生产量是否与年龄有关，现采用分层抽样的方法，从中抽取了100名工人，先统计了他们某月的日平均生产件数，然后按工人年龄在“25周岁以上（含25周岁）”和“25周岁以下”分为两组，再将两组工人的日平均生产件数分为5组：
[50，60），[60，70），[70，80），[80，90），[90，100）分别加以统计，得到如图所示的频率分布直方图．

（1）从样本中日平均生产件数不足60件的工人中随机抽取2人，求至少抽到一名“25周岁以下组”工人的概率．
（2）规定日平均生产件数不少于80件者为“生产能手”，请你根据已知条件完成2×2列联表，并判断是否能在犯错误的概率不超过0.1的前提下认为“生产能手与工人所在的年龄组有关”？（X²=$\frac{n（{n}_{11}{n}_{22}-{n}_{12}{n}_{21}）^{2}}{{n}_{1+}{n}_{2+}{n}_{+2}{n}_{+1}}$，X²＞6.635时有99%的把握具有相关性）

Answer 1

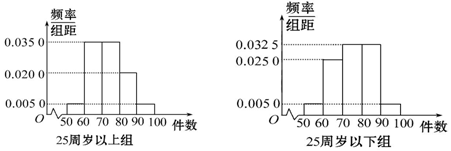
分析 （1）由分层抽样的特点可得样本中有25周岁以上、下组工人人数，再由所对应的频率可得样本中日平均生产件数不足60件的工人中，25周岁以上、下组工人的人数分别为3，2，由古典概型的概率公式可得答案；
（2）由频率分布直方图可得“25周岁以上组”中的生产能手的人数，以及“25周岁以下组”中的生产能手的人数，据此可得2×2列联表，可得k²≈1.79，由1.79＜2.706，可得结论．

解答 解：（1）由已知得，样本中有25周岁以上组工人60名，25周岁以下组工人40名，
所以，样本中日平均生产件数不足60件的工人中，25周岁以上组工人有60×0.05=3（人），记为A₁，A₂，A₃.25周岁以下组工人有40×0.05=2（人），记为B₁，B₂．
从中随机抽取2名工人，所有可能的结果共有10种，即：（A₁，A₂），（A₁，A₃），（A₂，A₃），（A₁，B₁），（A₁，B₂），（A₂，B₁），（A₂，B₂），（A₃，B₁），（A₃，B₂） （B₁，B₂）．其中，至少抽到一名“25周岁以下组”工人的可能结果共有7种，是：（A₁，B₁），（A₁，B₂），（A₂，B₁），（A₂，B₂），（A₃，B₁），（A₃，B₂），（B₁，B₂）．
故所求概率P=0.7．
（2）由频率分布直方图可知，在抽取的100名工人中，“25周岁以上组”中的生产能手有60×0.25=15（人），“25周岁以下组”中的生产能手有40×0.375=15（人），据此可得2×2列联表如下：

	生产能手	非生产能手	总计
25周岁以上组	15	45	60
25周岁以下组	15	25	40
总计	30	70	100

所以得：X²=$\frac{100×（15×25-15×45）^{2}}{60×40×30×70}$≈1.79．
所以不能在犯错误的概率不超过0.1的前提下认为“生产能手与工人所在的年龄组有关”．

点评 本题考查独立性检验，涉及频率分布直方图，以及古典概型的概率公式，属中档题．