
【题目】已知点![]() 在曲线
在曲线![]() 上,⊙
上,⊙![]() 过原点
过原点![]() ,且与
,且与![]() 轴的另一个交点为
轴的另一个交点为![]() ,若线段
,若线段![]() ,⊙
,⊙![]() 和曲线
和曲线![]() 上分别存在点
上分别存在点![]() 、点
、点![]() 和点
和点![]() ,使得四边形
,使得四边形![]() (点
(点![]() ,
, ![]() ,
, ![]() ,
, ![]() 顺时针排列)是正方形,则称点
顺时针排列)是正方形,则称点![]() 为曲线
为曲线![]() 的“完美点”.那么下列结论中正确的是( ).
的“完美点”.那么下列结论中正确的是( ).
A. 曲线![]() 上不存在”完美点”
上不存在”完美点”
B. 曲线![]() 上只存在一个“完美点”,其横坐标大于
上只存在一个“完美点”,其横坐标大于![]()
C. 曲线![]() 上只存在一个“完美点”,其横坐标大于
上只存在一个“完美点”,其横坐标大于![]() 且小于
且小于![]()
D. 曲线![]() 上存在两个“完美点”,其横坐标均大于
上存在两个“完美点”,其横坐标均大于![]()
科目:高中数学 来源: 题型:
【题目】【题目】【2018江西莲塘一中、临川二中高三上学期第一次联考】二次函数![]() 的图象过原点,对
的图象过原点,对![]() ,恒有
,恒有![]() 成立,设数列
成立,设数列![]() 满足
满足![]() .
.
(I)求证:对![]() ,恒有
,恒有![]() 成立;
成立;
(II)求函数![]() 的表达式;
的表达式;
(III)设数列![]() 前
前![]() 项和为
项和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
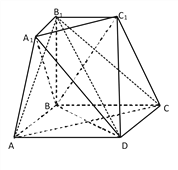
【题目】如图所示的几何体是由棱台![]() 和棱锥
和棱锥![]() 拼接而成的组合体,其底面四边形
拼接而成的组合体,其底面四边形![]() 是边长为
是边长为![]() 的菱形,且
的菱形,且![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() .
.
(1)求证:平面![]()
![]() 平面
平面![]()
![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在坐标原点![]() ,焦点在
,焦点在![]() 轴上,短轴长为
轴上,短轴长为![]() ,且两个焦点和短轴的两个端点恰为一个正方形的顶点,过右焦点
,且两个焦点和短轴的两个端点恰为一个正方形的顶点,过右焦点![]() 与
与![]() 轴不垂直的直线交椭圆于
轴不垂直的直线交椭圆于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的方程.
(Ⅱ)当直线![]() 的斜率为
的斜率为![]() 时,求
时,求![]() 的面积.
的面积.
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得经
,使得经![]() ,
, ![]() 为领边的平行四边形是菱形?若存在,求出
为领边的平行四边形是菱形?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线l过点P(-3,2),倾斜角为![]() ,且
,且![]() .曲线C的参数方程为
.曲线C的参数方程为![]() (
(![]() 为参数).直线l与曲线C交于A、B两点,线段AB的中点为M.
为参数).直线l与曲线C交于A、B两点,线段AB的中点为M.
(Ⅰ)求直线l的参数方程和曲线C的普通方程;
(Ⅱ)求线段PM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com