
【题目】椭圆![]() 上一点
上一点![]() 关于原点的对称点为
关于原点的对称点为![]() ,
, ![]() 为其右焦点,若
为其右焦点,若![]() ,设
,设![]() ,且
,且![]() ,则该椭圆离心率的最大值为( )
,则该椭圆离心率的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
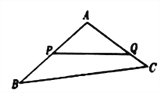
【题目】如图,某生态园将一块三角形地![]() 的一角
的一角![]() 开辟为水果园,已知角
开辟为水果园,已知角![]() 为
为![]() ,
, ![]() 的长度均大于200米,现在边界
的长度均大于200米,现在边界![]() 处建围墙,在
处建围墙,在![]() 处围竹篱笆.
处围竹篱笆.
(1)若围墙![]() 、
、![]() 总长度为200米,如何可使得三角形地块
总长度为200米,如何可使得三角形地块![]() 面积最大?
面积最大?
(2)已知竹篱笆长为![]() 米,
米, ![]() 段围墙高1米,
段围墙高1米, ![]() 段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)令![]() ,其图象上存在一点
,其图象上存在一点![]() ,使此处切线的斜率
,使此处切线的斜率![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)当![]() ,
, ![]() 时,方程
时,方程![]() 有唯一实数解,求正数
有唯一实数解,求正数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在曲线
在曲线![]() 上,⊙
上,⊙![]() 过原点
过原点![]() ,且与
,且与![]() 轴的另一个交点为
轴的另一个交点为![]() ,若线段
,若线段![]() ,⊙
,⊙![]() 和曲线
和曲线![]() 上分别存在点
上分别存在点![]() 、点
、点![]() 和点
和点![]() ,使得四边形
,使得四边形![]() (点
(点![]() ,
, ![]() ,
, ![]() ,
, ![]() 顺时针排列)是正方形,则称点
顺时针排列)是正方形,则称点![]() 为曲线
为曲线![]() 的“完美点”.那么下列结论中正确的是( ).
的“完美点”.那么下列结论中正确的是( ).
A. 曲线![]() 上不存在”完美点”
上不存在”完美点”
B. 曲线![]() 上只存在一个“完美点”,其横坐标大于
上只存在一个“完美点”,其横坐标大于![]()
C. 曲线![]() 上只存在一个“完美点”,其横坐标大于
上只存在一个“完美点”,其横坐标大于![]() 且小于
且小于![]()
D. 曲线![]() 上存在两个“完美点”,其横坐标均大于
上存在两个“完美点”,其横坐标均大于![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程选讲
在直角坐标系![]() 中,曲线C1的参数方程为
中,曲线C1的参数方程为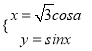 (a为参数),以原点O为极点,
(a为参数),以原点O为极点,
以x轴正半轴为极轴,建立极坐标系,曲 线C2的极坐标方程为![]()
(1)求曲线C1的普通方程与曲线C2的直角坐标方程.
(2)设P为曲线C1上的动点,求点P到C2上点的距离的最小值,并求此时点P坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年全国数学奥赛试行改革:在高二一年中举行5次全区竞赛,学生如果其中2次成绩达全区前20名即可进入省队培训,不用参加其余的竞赛,而每个学生最多也只能参加5次竞赛.规定:若前4次竞赛成绩都没有达全区前20名,则第5次不能参加竞赛.假设某学生每次成绩达全区前20名的概率都是![]() ,每次竞赛成绩达全区前20名与否互相独立.
,每次竞赛成绩达全区前20名与否互相独立.
(1)求该学生进入省队的概率.
(2)如果该学生进入省队或参加完5次竞赛就结束,记该学生参加竞赛的次数为![]() ,求
,求![]() 的分布列及
的分布列及![]() 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com