
分析 由题意可求得数列的通项公式,解不等式可得前8项为正数,第9项为0,从第10项开始为负数,易得结论.
解答 解:∵等差数列{an}中a1=4,a3=3,
∴公差d=$\frac{1}{2}$(a3-a1)=-$\frac{1}{2}$,
∴an=4-$\frac{1}{2}$(n-1)=$\frac{1}{2}$(9-n),
令an=$\frac{1}{2}$(9-n)≤0可得n≥9,
故等差数列{an}的前8项为正数,第9项为0,从第10项开始为负数,
∴当n=8或9时,Sn最大.
故答案为:8或9
点评 本题考查等差数列前n项和的最值,从数列项的正负变换入手是解决问题的关键,属基础题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{π}{6}$) | B. | ($\frac{π}{6}$,π) | C. | [$\frac{π}{3}$,π) | D. | (0,$\frac{π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | -$\frac{5}{4}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{1}=1$ | D. | ${x^2}-\frac{y^2}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
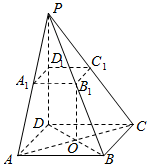 在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.
在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com