
已知函数f(x)=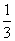 x3-x,数列{an}满足条件:a1≥1,an+1≥f ′(an+1).
x3-x,数列{an}满足条件:a1≥1,an+1≥f ′(an+1).
试比较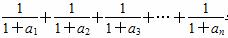 与1的大小,并说明理由.
与1的大小,并说明理由.
∵f ′(x)=x2-1,an+1≥f ′(an+1),
∴an+1≥(an+1)2-1.
∵函数g(x)=(x+1)2-1=x2+2x在区间[-1,+∞)上单调递增,于是由a1≥1,及a2≥(a1+1)2-1得,a2≥22-1,进而得a3≥(a2+1)2-1≥24-1>23-1,
由此猜想:an≥2n-1.
下面用数学归纳法证明这个猜想:
①当n=1时,a1≥21-1=1,结论成立;
②假设当n=k(k≥1且k∈N*)时结论成立,即ak≥2k-1,则当n=k+1时,由g(x)=(x+1)2-1在区间[-1,+∞)上单调递增知,ak+1≥(ak+1)2-1≥22k-1≥2k+1-1,
即n=k+1时,结论也成立.
由①②知,对任意n∈N*,都有an≥2n-1.


科目:高中数学 来源: 题型:
有一批货物需要用汽车从城市甲运至城市乙,已知从城市甲到城市乙只有两条公路,且通过这两条公路所用的时间互不影响.据调查统计,通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布如下表:
| 所用的时间(天数) | 10 | 11 | 12 | 13 |
| 通过公路1的频数 | 20 | 40 | 20 | 20 |
| 通过公路2的频数 | 10 | 40 | 40 | 10 |
假设汽车A只能在约定日期(某月某日)的前11天出发,汽车B只能在约定日期的前12天出发.
(1)为了尽最大可能在各自允许的时间内将货物运往城市乙,估计汽车A和汽车B应如何选择各自的路径.
(2)若通过公路1、公路2的“一次性费用”分别为3.2万元、1.6万元(其他费用忽略不计),此项费用由生产商承担.如果生产商恰能在约定日期当天将货物送到,则销售商一次性支付给生产商40万元,若在约定日期前送到,每提前一天销售商将多支付给生产商2万元;若在约定日期后送到,每迟到一天,销售商将少支付给生产商2万元.如果汽车A、B长期按(1)中所选路径运输货物,试比较哪辆汽车为生产商获得的毛利润更大.
(注:毛利润=销售商支付给生产商的费用-一次性费用)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(n)=1+ +
+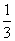 +…+
+…+ (n∈N*),经计算得f(2)=
(n∈N*),经计算得f(2)=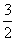 ,f(4)>2,f(8)>
,f(4)>2,f(8)>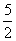 ,f(16)>3,f(32)>
,f(16)>3,f(32)>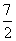 .则有________________.
.则有________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
对于大于或等于2的自然数n的二次方幂有如下分解方式:22=1+3,32=1+3+5,42=1+3+5+7,…,根据上述分解规律,对任意自然数n,当n≥2时,有____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
数列{an}中,已知a1=1,当n≥2时,an-an-1=2n-1,依次计算a2、a3、a4后,猜想an的表达式是( )
A.an=3n-2 B.an=n2
C.an=3n-1 D.an=4n-3
查看答案和解析>>
科目:高中数学 来源: 题型:
对于不等式 ≤n+1(n∈N*),某人的证明过程如下:
≤n+1(n∈N*),某人的证明过程如下:
1°当n=1时,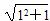 ≤1+1,不等式成立.
≤1+1,不等式成立.
2°假设n=k(k∈N*)时不等式成立,即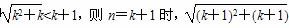 =
=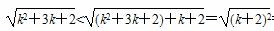 =(k+1)+1.
=(k+1)+1.
∴当n=k+1时,不等式成立.
上述证法( )
A.过程全都正确
B.n=1验得不正确
C.归纳假设不正确
D.从n=k到n=k+1的推理不正确
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在△ABC中,∠A=90°,正方形DEFG的边长是6cm,且四个顶点都在△ABC的各边上,CE=3 cm,则BC的长为( )
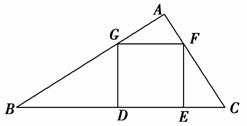
A.12cm B.21cm
C.18cm D.15cm
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线C1: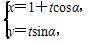 (t为参数),圆C2:
(t为参数),圆C2: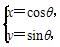 (θ为参数).
(θ为参数).
(1)当α=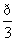 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标;
(2)过坐标原点O作C1的垂线,垂足为A,P为OA的中点.当α变化时,求P点轨迹的参数方程,并指出它是什么曲线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com