

分析 由已知中的数阵,可得第n行的第一个数和最后一个数均为:$\frac{2}{(n+1)(n+2)}$,其它数字等于上一行该数字“肩膀“上两个数字的和,结合裂项相消法,可得答案.
解答 解:由已知条件中的数阵归纳可得,第n行的第一个数和最后一个数均为:$\frac{2}{(n+1)(n+2)}$,其它数字等于上一行该数字“肩膀“上两个数字的和,
故A(15,2)=$\frac{1}{6}+\frac{1}{6}+\frac{1}{10}+\frac{1}{15}$+…+$\frac{2}{15×16}$=$\frac{1}{6}$+2($\frac{1}{3}-\frac{1}{16}$)=$\frac{17}{24}$,
故答案为:$\frac{17}{24}$.
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


科目:高中数学 来源: 题型:选择题
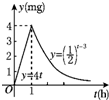 某医药研究所研发出一种新药,成年人按规定的剂量服用后,据检测,每毫升血液中的含药量y(mg)与时间t(h)之间的关系如图所示.据进一步测定,当每毫升血液中的含药量不少于0.25mg时,治疗疾病有效,则服药一次,治疗疾病有效的时间为( )
某医药研究所研发出一种新药,成年人按规定的剂量服用后,据检测,每毫升血液中的含药量y(mg)与时间t(h)之间的关系如图所示.据进一步测定,当每毫升血液中的含药量不少于0.25mg时,治疗疾病有效,则服药一次,治疗疾病有效的时间为( )| A. | 4 h | B. | 4$\frac{7}{8}$ h | C. | 4$\frac{15}{16}$ h | D. | 5 h |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1+a3≥2a2 | B. | 若a3>a1,则a4>a2 | C. | 若a1=a3,则a1=a2 | D. | a12+a32≥2a22 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 用电量(度) | (0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
| 户数 | 5 | 15 | 10 | 15 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com