
分析 通过对an-1-an=2an•an-1(n≥2,n∈N*)变形可得数列{$\frac{1}{{a}_{n}}$}是以3为首项、2为公差的等差数列,计算可得通项,再利用拆项法、并项相加即得结论.
解答 解:∵an-1-an=2an•an-1(n≥2,n∈N*),an≠0,
∴2=$\frac{{a}_{n-1}-{a}_{n}}{{a}_{n}•{a}_{n-1}}$=$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$,
又∵a1=$\frac{1}{3}$,∴$\frac{1}{{a}_{1}}$=3,
∴数列{$\frac{1}{{a}_{n}}$}是以3为首项、2为公差的等差数列,
∴$\frac{1}{{a}_{n}}$=3+2(n-1)=2n+1,
∴an=$\frac{1}{2n+1}$;
∴an•an+1=$\frac{1}{2n+1}•\frac{1}{2n+3}$=$\frac{1}{2}$($\frac{1}{2n+1}$-$\frac{1}{2n+3}$),
∴a1a2+a2a3+…+a99a100=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{197}$-$\frac{1}{199}$+$\frac{1}{199}$-$\frac{1}{201}$)
=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{201}$)=$\frac{11}{67}$,
故答案为:$\frac{1}{2n+1}$,$\frac{11}{67}$.
点评 本题考查求数列的通项,对表达式的灵活变形和并项相加法是解决本题的关键,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 题 | A | B | C |
| 答卷数 | 180 | 300 | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
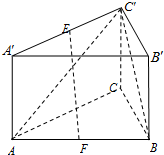 如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.
如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com