
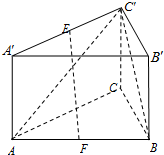
 如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.
如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.分析 (1)根据线面垂直的判定定理证明AC⊥BC,即可证明BC⊥平面ACC′A′;
(2)根据线面平行的判定定理证明EF∥BG即可证明EF∥平面BCC′B′;
(3)根据二面角的定义先求出二面角的平面角,结合三角形的边角关系即可求tanθ的值.
解答 (1)证明:∵CC′⊥底面ABC,
∴CC′⊥BC
∵∠ACB=90°,∴AC⊥BC,
又AC∩CC′=C,
∴BC⊥平面ACC′A.
(2)证明:取B′C′的中点G,连接EG、BG,
又E是A′C′的中点,
则EG∥A′B′且等于A′B′的一半.
ABCEFG
∵F是AB中点,
∴BF∥A′B′且等于A′B′的一半,
∴EG与BF平行且相等.
∴四边形EGBF是平行四边形,∴EF∥BG,
又EF?平面BCC′B′,BG?平面BCC′B′,
∴EF∥平面BCC′B′
(3)解:连接FC、FC′.
∵AC=BC,F是AB中点,
∴CF⊥AB,
又∵CC′⊥底面ABC,
∴CC′⊥AB,
∴AB⊥平面CFC′,
∴C′F⊥AB,
∴∠C′FC为二面角C′-AB-C的平面角,
即θ=∠C′FC,
在Rt△ABC中,∠ACB=90°,AC=BC=a,F是AB中点,
∴CF=$\frac{\sqrt{2}}{2}a$,
又△C′FC是直角三角形,且∠C′CF=90°,CC′=a,
∴tanθ=tan∠C′FC=$\frac{a}{\frac{\sqrt{2}a}{2}}=\sqrt{2}$.
点评 本题主要考查线面平行和垂直的判定,以及二面角的求解,要求熟练掌握相应的判定定理以及,利用向量法求解二面角的大小.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:填空题
 用红、黄、蓝、绿、紫五种不同的颜色填充到如图所示的图形中,每格只填一种颜色,相邻两格不同色,记ξ为填充色为红色的格数,则P(ξ=2)=$\frac{6}{35}$.
用红、黄、蓝、绿、紫五种不同的颜色填充到如图所示的图形中,每格只填一种颜色,相邻两格不同色,记ξ为填充色为红色的格数,则P(ξ=2)=$\frac{6}{35}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com