
分析 (1)先求导,根据导数的几何意义,得到k的表达式,再根据二次函数的性质,求出k的取值范围;
(2)由(1)知,函数f(x)在(-1,1)单调递增,即得到k>0,构造函数令h(x)=f(x)-kx,则h(x1)=h(x2),利用导数和函数的极值的关系,求证得到h(x0)为h(x)的唯一极大值,问题得以证明.
解答 解:(1)f′(x)=$\frac{ab-a{x}^{2}}{({x}^{2}+b)^{2}}$,
由f′(1)=0,即f(1)=2,解得a=4,b=1,
∴k=f′(x0)=4[$\frac{2}{(1+{{x}_{0}}^{2})^{2}}$-${\frac{1}{1+{{x}_{0}}^{2}}}^{\;}$],
设t=$\frac{1}{1+{{x}_{0}}^{2}}$,t∈(0,1],
∴k=4(2t2-1)=8(t-$\frac{1}{4}$)2-$\frac{1}{2}$,
∵k=4(2t2-t)=8(t-$\frac{1}{4}$)2-$\frac{1}{2}$在(0,$\frac{1}{4}$]上为减函数,在($\frac{1}{4}$,1]上为增函数,
当t=$\frac{1}{4}$时,k有最小值为-$\frac{1}{2}$,当x=1时,有最大值为4,
∴k∈[$-\frac{1}{2}$,4];
(2)证明:由(1)知f′(x)=$\frac{4-4{x}^{2}}{(1+{x}^{2})^{2}}$,
令f′(x)>0,解得-1<x<1,函数f(x)在(-1,1)单调递增,
∵0<x1<x2<1,
∴k=$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$>0,
∴x0∈(-1,1)
∵f′(x0)=f′(-x0),
故只需要证明x0∈(0,1)时结论成立,
∵k=$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$,
∴f(x2)-kx2=f(x1)-kx1,
令h(x)=f(x)-kx,则h(x1)=h(x2),
∴h′(x)=f′(x)-k,则h′(x0)=0
设g(x)=$\frac{1-x}{(1+x)^{2}}$,x∈(0,1),
∴g′(x)=$\frac{x-3}{(1+x)^{3}}$<0,
∴g(x)为减函数,
∴f′(x)为减函数,
∴当x>x0时,有f′(x)<f′(x0)=k,此时h′(x)<0,h(x)为减函数,
当x<x0时,h′(x)>0,h(x)为增函数,
∴h(x0)为h(x)的唯一极大值,
因此要使h(x1)=h(x2),必有证x1<x0<x2.
综上,有x1<|x|<x2.
点评 本题考查了导数的几何意义,以及导数和函数的极值的关系,关键是构造函数,培养可学生得转化能力,运算能力,属于难题.


科目:高中数学 来源: 题型:解答题
| 题 | A | B | C |
| 答卷数 | 180 | 300 | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
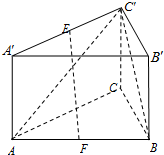 如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.
如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中有一椭圆,椭圆方程为C:$\frac{{x}^{2}}{2}+{y}^{2}$=1.左右焦点分别F1(-1,0)和(1,0).设A,B是椭圆上位于x轴上方的两点,且直线AF1与直线BF2平行,AF2与BF1交于点P.求证:PF1+PF2是定值.
如图,在平面直角坐标系xOy中有一椭圆,椭圆方程为C:$\frac{{x}^{2}}{2}+{y}^{2}$=1.左右焦点分别F1(-1,0)和(1,0).设A,B是椭圆上位于x轴上方的两点,且直线AF1与直线BF2平行,AF2与BF1交于点P.求证:PF1+PF2是定值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在如图所示的几何体中,四边形ABCD是矩形,AB=2BC=4,四边形CDEF是等腰梯形,EF∥DC,EF=2,且平面ABCD⊥平面CDEF,AF⊥CF.
在如图所示的几何体中,四边形ABCD是矩形,AB=2BC=4,四边形CDEF是等腰梯形,EF∥DC,EF=2,且平面ABCD⊥平面CDEF,AF⊥CF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 做不到光盘 | 能做到光盘 | 合计 | |
| 男 | 45 | 10 | 55 |
| 女 | 30 | 15 | 45 |
| 合计 | 70 | 25 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com