
分析 (1)运用导数的公式和导数的运算法则,求得函数的导数;
(2)令导数为0,求得方程的解,注意定义域的运用,求得极值和端点处的函数值,即可得到最值.
解答 解:(1)函数f(x)=$\frac{1}{3}$x3-4x的导数f′(x)=x2-4;
(2)由f′(x)=x2-4=0,解得x=2(-2舍去),
由f(0)=0,f(2)=$\frac{8}{3}$-8=-$\frac{16}{3}$,f(3)=9-12=-3,
即有f(x)在闭区间[0,3]上的最大值为0,最小值为-$\frac{16}{3}$.
点评 本题考查导数的运用:求最值,主要考查求最值的方法,注意函数的定义域的运用,属于基础题.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:解答题
 某校在一次数学考试中随机抽取了N名学生的成绩并分成一下五组,第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,已知图中从左到右后3个小组的频率之比为3:2:1,其中第4组的频数为20.
某校在一次数学考试中随机抽取了N名学生的成绩并分成一下五组,第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,已知图中从左到右后3个小组的频率之比为3:2:1,其中第4组的频数为20.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知平行四边形ABCD(如图1),AB=4,AD=2,∠DAB=60°,E为AB的中点,把三角形ADE沿DE折起至A1DE位置,使得A1C=4,F是线段A1C的中点(如图2).
已知平行四边形ABCD(如图1),AB=4,AD=2,∠DAB=60°,E为AB的中点,把三角形ADE沿DE折起至A1DE位置,使得A1C=4,F是线段A1C的中点(如图2).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
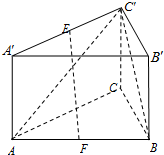 如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.
如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中有一椭圆,椭圆方程为C:$\frac{{x}^{2}}{2}+{y}^{2}$=1.左右焦点分别F1(-1,0)和(1,0).设A,B是椭圆上位于x轴上方的两点,且直线AF1与直线BF2平行,AF2与BF1交于点P.求证:PF1+PF2是定值.
如图,在平面直角坐标系xOy中有一椭圆,椭圆方程为C:$\frac{{x}^{2}}{2}+{y}^{2}$=1.左右焦点分别F1(-1,0)和(1,0).设A,B是椭圆上位于x轴上方的两点,且直线AF1与直线BF2平行,AF2与BF1交于点P.求证:PF1+PF2是定值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com