
分析 数字1,2,3,4,5任意排成一列,其基本事件的总数为:${A}_{5}^{5}$,有1个巧合,即为有一个数字恰好在其位置,其他4个数字均不在对应位置,依次求出巧合数为1的情况,进而得出P(ξ=1).
解答 解:(1)数字1,2,3,4,5任意排成一列,其基本事件的总数为:${A}_{5}^{5}$,
ξ=5时,5个数字均在对应位置,有1种情况,P(ξ=5)=$\frac{1}{{A}_{5}^{5}}$=$\frac{1}{120}$;
ξ=4,4个数字在对应位置,不可能出现,P(ξ=4)=0;
ξ=3,有3个数在对应位置,另外2个数互换位置,P(ξ=3)=$\frac{{C}_{5}^{3}}{{A}_{5}^{5}}$=$\frac{10}{120}$;
ξ=2,有2个数在对应位置,另外3个数不在对应位置,P(ξ=2)=$\frac{{C}_{5}^{2}×2}{{A}_{5}^{5}}$=$\frac{20}{120}$;
ξ=1,有1个数在对应位置,另外4个数不在对应位置,P(ξ=1)=$\frac{{C}_{5}^{1}×3×3}{{A}_{5}^{5}}$=$\frac{45}{120}$;
ξ=0,所有5个数均不在对应位置,P(ξ=0)=$\frac{4×[2+3×(1+2)]}{{A}_{5}^{5}}$=$\frac{44}{120}$;
所以,巧合数ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | 5 |
| P | $\frac{44}{120}$ | $\frac{45}{120}$ | $\frac{20}{120}$ | $\frac{10}{120}$ | $\frac{1}{120}$ |
点评 本题考查随机变量的分布列与数学期望,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 政府向市民宣传绿色出行(即乘公共汽车、地铁或步行出行),并进行广泛动员,三个月后,统计部门在一个小区随机抽取了100户家庭,调查了他们在政府动员后三个月的月平均绿色出行次数(单位:次),将所得数据分组,画出频率分布直方图(如图所示).
政府向市民宣传绿色出行(即乘公共汽车、地铁或步行出行),并进行广泛动员,三个月后,统计部门在一个小区随机抽取了100户家庭,调查了他们在政府动员后三个月的月平均绿色出行次数(单位:次),将所得数据分组,画出频率分布直方图(如图所示).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
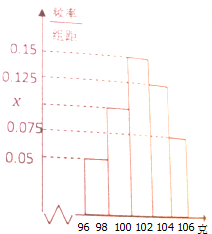 某工厂从一批产品中随机抽取40件进行检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).
某工厂从一批产品中随机抽取40件进行检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com