
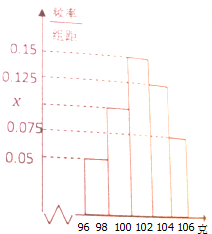
 某工厂从一批产品中随机抽取40件进行检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).
某工厂从一批产品中随机抽取40件进行检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).分析 (1)由频率分布直方图的性质可得:2×(0.05+x+0.15+0.125+0.075)=1,解得x即可.
(2)产品的净重在[98,100)中的共有0.1×2×40=8件.可得至少有2件产品的净重在[98,100)中的概率P=$\frac{{8}^{2}×32}{4{0}^{3}}$.
(3)由题意可得ξ=0,1,2.产品净重在[98,104)的共有2×(1-0.05-0.075)×40=30.利用“超几何分布”即可得出.
解答 解:(1)由频率分布直方图的性质可得:2×(0.05+x+0.15+0.125+0.075)=1,解得x=0.1.
(2)产品的净重在[98,100)中的共有0.1×2×40=8件.
∴至少有2件产品的净重在[98,100)中的概率P=$\frac{{8}^{2}×32}{4{0}^{3}}$=$\frac{4}{125}$.
(3)由题意可得ξ=0,1,2.
产品净重在[98,104)的共有2×(1-0.05-0.075)×40=30.
则P(ξ=0)=$\frac{{∁}_{10}^{2}}{{∁}_{40}^{2}}$=$\frac{3}{52}$,P(ξ=1)=$\frac{{∁}_{30}^{1}{∁}_{10}^{1}}{{∁}_{40}^{2}}$=$\frac{5}{13}$,P(ξ=2)=$\frac{{∁}_{30}^{2}}{{∁}_{40}^{2}}$=$\frac{29}{52}$.
∴ξ的分布列为:
| ξ | 1 | 2 | 3 |
| P | $\frac{3}{52}$ | $\frac{5}{13}$ | $\frac{29}{52}$ |
点评 本题考查了频率分布直方图的性质、组合数的计算公式、古典概率计算公式、“超几何分布”的分布列与数学期望,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 已知平行四边形ABCD(如图1),AB=4,AD=2,∠DAB=60°,E为AB的中点,把三角形ADE沿DE折起至A1DE位置,使得A1C=4,F是线段A1C的中点(如图2).
已知平行四边形ABCD(如图1),AB=4,AD=2,∠DAB=60°,E为AB的中点,把三角形ADE沿DE折起至A1DE位置,使得A1C=4,F是线段A1C的中点(如图2).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{3}$ | a | $\frac{1}{4}$ | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知AB⊥平面BEC,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形.
如图,已知AB⊥平面BEC,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com