
分析 (Ⅰ)根据题意直接可得结论;
(Ⅱ)通过分析可得a1=a2=1,a3=a4=2,…,a2n-1=a2n=n,…分n为奇数、偶数两种情况考虑即可;
(Ⅲ)考查符合条件的数列P中,存在某个i(i≤i≤19)满足ai≤ai+1,通过Tk(P)=min{n|an≥k}(k∈N*),可得${T}_{{a}_{i}+1}$(P)=i+1,故只需将数列P略作调整,仅将第ai的值增加1,即调整后s′=s.如果数列{an′}还有存在相邻两项不相等,继续做以上的操作,最终一定可以经过有限次的操作,使得{an}中的每一项变为相等,且操作中保持s的值不变,计算即可.
解答 解:(Ⅰ)∵数列P:1?3?4?7?…,即从第三项起每项是前两项的和,
∴T1(P)=1,T2(P)=2,T3(P)=2,T4(P)=3,T5(P)=4;
(Ⅱ)∵Tk(P)=2k-1,
∴T1(P)=1,T2(P)=3,T3(P)=5,T4(P)=7,…
∵T2(P)=3,且Tk(P)=min{n|an≥k}(k∈N*),
∴a3≥2,且a2<2,
同理,由T3(P)=5,且Tk(P)=min{n|an≥k}(k∈N*),
得a5≥3,a4<3,
以此类推,得a7≥4,a6<4;…;a2n-1≥n,a2n-2<n;…
∵ai≤ai+1(i∈N*),ai∈N*,
∴a1=a2=1,a3=a4=2,…,a2n-1=a2n=n,…
当n为奇数时,a1+a2+a3+…+an=2(1+2+…+$\frac{n-1}{2}$)+$\frac{n+1}{2}$=$\frac{(n+1)^{2}}{4}$,
当n为偶数时,a1+a2+a3+…+an=2(1+2+…+$\frac{n}{2}$)=$\frac{{n}^{2}+2n}{4}$,
∴数列{an}前n项的和Sn=$\left\{\begin{array}{l}{\frac{(n+1)^{2}}{4},}&{n为奇数}\\{\frac{{n}^{2}+2n}{4},}&{n为偶数}\end{array}\right.$;
(Ⅲ)考查符合条件的数列P中,
若存在某个i(1≤i≤19)满足ai≤ai+1,
对应可得Tk(P),及s=a1+a2+…+a20+T1(P)+T2(P)+…+T46(P).
∵Tk(P)=min{n|an≥k}(k∈N*),∴${T}_{{a}_{i}+1}$(P)=i+1,
下面将数列P略作调整,仅将第ai的值增加1,具体如下:
将aj′=aj+1,对于任何j(j≠1)令aj′=aj,可得数列P′及其对应数列Tk(P′),
根据数列Tk(P′)的定义,可得${T}_{{a}_{i}+1}$(P′)=i,且Tj(P′)=Tj(P)(j≠ai+1).
显然${T}_{{a}_{i}+1}$(P′)=${T}_{{a}_{i}+1}$(P)-1,
∴s′=a1′+a2′+…+a20′+T1(P′)+T2(P′)+…+T46(P′)
=a1+a2+…+ai-1+(ai+1)+ai+1+…+a20+T1(P)+T2(P)+…+(${T}_{{a}_{i}+1}$-1)+${T}_{{a}_{i}+2}$+…+T46(P)
=a1+a2+…+a20+T1(P)+T2(P)+…+T46(P)=s,
即调整后s′=s.
如果数列{an′}还有存在相邻两项不相等,继续做以上的操作,
最终一定可以经过有限次的操作,使得{an}中的每一项变为相等,
且操作中保持s的值不变,
而当a1=a2=…=a20=46时,T1(P)=T2(P)=…=T46(P)=1,
∴s=a1+a2+…+a20+T1(P)+T2(P)+…+T46(P)=46×20+46=966.
点评 本题是一道建立在数列上的新定义题,考查分类讨论的思想,考查分析问题、解决问题的能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
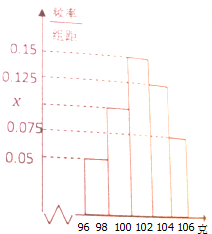 某工厂从一批产品中随机抽取40件进行检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).
某工厂从一批产品中随机抽取40件进行检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{6}{5}$ | C. | 2 | D. | 6$\sqrt{2}$-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com