
 用红、黄、蓝、绿、紫五种不同的颜色填充到如图所示的图形中,每格只填一种颜色,相邻两格不同色,记ξ为填充色为红色的格数,则P(ξ=2)=$\frac{6}{35}$.
用红、黄、蓝、绿、紫五种不同的颜色填充到如图所示的图形中,每格只填一种颜色,相邻两格不同色,记ξ为填充色为红色的格数,则P(ξ=2)=$\frac{6}{35}$. 分析 设M表示事件“恰有两个区域用红色填充”:当区域1、4同色时,共有5×4×3×1×3=180种;当区域1、4不同色时,共有5×4×3×2×2=240种;可得所有基本事件总数为:180+240,求出1、4为红色时,2、5为红色时,即可得出.
解答 解:设M表示事件“恰有两个区域用红色填充”:
当区域1、4同色时,共有5×4×3×1×3=180种;
当区域1、4不同色时,共有5×4×3×2×2=240种;
因此,所有基本事件总数为:180+240=420种
又∵1、4为红色时,共有4×3×3=36种;
2、5为红色时,共有4×3×3=36种;
因此,事件M包含的基本事件有:36+36=72种
∴恰有两个区域用红色填充的概率P(M)=P(ξ=2)=$\frac{72}{420}$=$\frac{6}{35}$.
点评 本题考查了排列组合数的计算公式、古典概率计算公式、分类讨论思想方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | [0+∞) | C. | [0,2] | D. | [1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 9 | C. | 18 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校在一次数学考试中随机抽取了N名学生的成绩并分成一下五组,第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,已知图中从左到右后3个小组的频率之比为3:2:1,其中第4组的频数为20.
某校在一次数学考试中随机抽取了N名学生的成绩并分成一下五组,第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,已知图中从左到右后3个小组的频率之比为3:2:1,其中第4组的频数为20.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 题 | A | B | C |
| 答卷数 | 180 | 300 | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
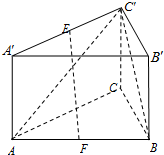 如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.
如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com