
分析 A表示“从甲盒、乙盒中各取1球颜色相同”,Bi表示“甲盒中有i只球”,i=0,1,2,3,4,先分别求出P(Bi),再由全概率公式求出P(A),然后由贝叶斯公式分别求出P(B1|A),P(B2|A),P(B3|A),从而得到放入甲盒中,2只白球的概率最大.
解答 解:A表示“从甲盒、乙盒中各取1球颜色相同”,
Bi表示“甲盒中有i只球”,i=0,1,2,3,4,由题意知A?$\sum_{i=1}^{3}{B}_{i}$,
P(B1)$\frac{{C}_{4}^{1}{C}_{4}^{3}}{{C}_{8}^{4}}$=$\frac{8}{35}$,P(A|B1)=$\frac{1}{4}×\frac{3}{4}+\frac{3}{4}×\frac{1}{4}=\frac{3}{8}$,
P(B2)=$\frac{{C}_{4}^{2}{C}_{4}^{2}}{{C}_{8}^{4}}$=$\frac{18}{35}$,P(A|B2)=$\frac{2}{4}×\frac{2}{4}+\frac{2}{4}×\frac{2}{4}$=$\frac{4}{8}$,
P(B3)=$\frac{{C}_{4}^{3}{C}_{4}^{1}}{{C}_{8}^{4}}$=$\frac{8}{35}$,P(A|B3)=$\frac{3}{4}×\frac{1}{4}+\frac{1}{4}×\frac{3}{4}$=$\frac{3}{8}$,
由全概率公式得:P(A)=$\sum_{k=1}^{3}P({B}_{k})P(A|{B}_{k})$=$\frac{8}{35}×\frac{3}{8}+\frac{18}{35}×\frac{4}{8}+\frac{8}{35}×\frac{3}{8}$=$\frac{3}{7}$.
由贝叶斯公式,得P(B1|A)=$\frac{P({B}_{1})P(A{|B}_{1})}{P(A)}$=$\frac{1}{5}$,
P(B2|A)=$\frac{P({B}_{2})P(A|{B}_{2})}{P(A)}$=$\frac{3}{5}$,
P(B3|A)=$\frac{P({B}_{3})P(A|{B}_{3})}{P(A)}$=$\frac{1}{5}$.
∴放入甲盒中,2只白球的概率最大.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意条件概率、全概率公式、贝叶斯公式的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
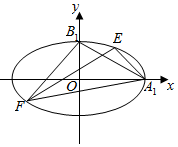 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,点E($\sqrt{3}$,$\frac{1}{2}$)在椭圆上,设点A1,B1分别是椭圆的右顶点和上顶点,过点A1,B1引椭圆C的两条弦A1E、B1F.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,点E($\sqrt{3}$,$\frac{1}{2}$)在椭圆上,设点A1,B1分别是椭圆的右顶点和上顶点,过点A1,B1引椭圆C的两条弦A1E、B1F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com