
分析 由于直线过定点M(3,1),点M在圆C:(x-1)2+(y-2)2=25的内部,故直线被圆截得的弦长最短时,CM垂直于直线l,根据它们的斜率之积等于-1求出m的值.
解答 解:直线l:(2m+1)x+(m+1)y-7m-4=0 即(x+y-4)+m(2x+y-7)=0,过定点M(3,1),
由于点M在圆C:(x-1)2+(y-2)2=25的内部,故直线被圆截得的弦长最短时,CM垂直于直线l,
故它们的斜率之积等于-1,即$\frac{1-2}{3-1}×(-\frac{2m+1}{m+1})$=-1,解得m=-$\frac{3}{4}$,
故答案为:-$\frac{3}{4}$.
点评 本题主要考查直线和圆的位置关系,直线过定点问题,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在边长是2的正方体ABCD-A1B1C1D1中,E,F分别为AB,A1C的中点.
如图,在边长是2的正方体ABCD-A1B1C1D1中,E,F分别为AB,A1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
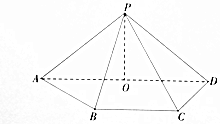 如图,四棱锥P-ABCD中,O为AD的中点,AD∥BC,CD⊥平面PAD,PA=PD=5.
如图,四棱锥P-ABCD中,O为AD的中点,AD∥BC,CD⊥平面PAD,PA=PD=5.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$-1 | D. | 2$\sqrt{2}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $-\frac{5}{12}$ | C. | $-\frac{12}{5}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,1]∪\left\{{\frac{3}{2}}\right\}$ | B. | $(0,\frac{3}{2}]$ | C. | $(0,1)∪\left\{{\frac{3}{2}}\right\}$ | D. | $(0,\frac{3}{2})∪\left\{0\right\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
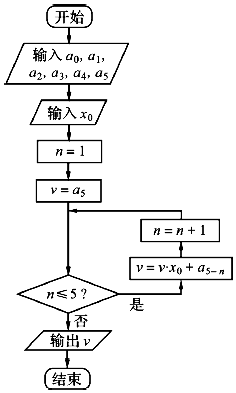 执行如图所示的程序框图,若输入a0=0,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出v的值为( )
执行如图所示的程序框图,若输入a0=0,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出v的值为( )| A. | 15 | B. | 3 | C. | -3 | D. | -15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
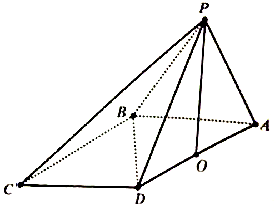 在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.
在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com