
【题目】已知![]() .
.
(1)若函数![]() 的单调递减区间为
的单调递减区间为![]() ,求函数
,求函数![]() 的图像在点
的图像在点![]() 处的切线方程;
处的切线方程;
(2)若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:⑴求出![]() 的导函数,令导函数小于
的导函数,令导函数小于![]() 得到不等式的解集,得到相应方程的两个根,将根代入求出
得到不等式的解集,得到相应方程的两个根,将根代入求出![]() 的值,得到函数
的值,得到函数![]() 的解析式,求出
的解析式,求出![]() 的导数在
的导数在![]() 的值即曲线的切线斜率,利用点斜式求出切线的方程
的值即曲线的切线斜率,利用点斜式求出切线的方程
⑵求出不等式,分离出参数![]() ,构造函数
,构造函数![]() ,利用导数求出
,利用导数求出![]() 的最大值,令
的最大值,令![]() 大于等于最大值,求出
大于等于最大值,求出![]() 的范围;
的范围;
解析:(1)![]() ,由题意,知
,由题意,知![]() 的解集是
的解集是![]() ,
,
即方程![]() 的两根分别是
的两根分别是![]() .
.
将![]() 或
或![]() 代入方程
代入方程![]() ,得
,得![]() ,
,
∴![]() ,
, ![]() ,∴
,∴![]() ,
,
∴![]() 的图像在点
的图像在点![]() 处的切线斜率
处的切线斜率![]() ,
,
∴函数![]() 的图像在点
的图像在点![]() 处的切线方程为:
处的切线方程为: ![]() ,即
,即![]() ;
;
(2)∵![]() 恒成立,
恒成立,
即![]() 对一切
对一切![]() 恒成立,
恒成立,
整理可得![]() 对一切
对一切![]() 恒成立,
恒成立,
设![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() (舍),
(舍),
当![]() 时,
时, ![]() 单调递增;当
单调递增;当![]() 时,
时, ![]() 单调递减,
单调递减,
∴当![]() 时,
时, ![]() 取得最大值
取得最大值![]() ,∴
,∴![]() .
.
故实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(1)写出价格![]() 关于时间
关于时间![]() 的函数关系式;(
的函数关系式;(![]() 表示投放市场的第
表示投放市场的第![]() 天);
天);
(2)销售量![]() 与时间
与时间![]() 的函数关系:
的函数关系:![]() ,则该产品投放市场第几天销售额最高?最高为多少千元?
,则该产品投放市场第几天销售额最高?最高为多少千元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() 方程
方程![]() 表示焦点在
表示焦点在![]() 轴上的椭圆;命题
轴上的椭圆;命题![]() 方程
方程![]() 表示的曲线是双曲线.
表示的曲线是双曲线.
(1)若“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若“![]() ”为假命题、且“
”为假命题、且“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且
,且![]() 在
在![]() 和
和![]() 处取得极值.
处取得极值.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)设函数![]() ,是否存在实数
,是否存在实数![]() ,使得曲线
,使得曲线![]() 与
与![]() 轴有两个交点,若存在,求出
轴有两个交点,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某粮库拟建一个储粮仓如图所示,其下部是高为2的圆柱,上部是母线长为2的圆锥,现要设计其底面半径和上部圆锥的高,若设圆锥的高![]() 为
为![]() ,储粮仓的体积为
,储粮仓的体积为![]() .
.
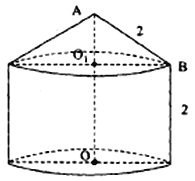
(1)求![]() 关于
关于![]() 的函数关系式;(圆周率用
的函数关系式;(圆周率用![]() 表示)
表示)
(2)求![]() 为何值时,储粮仓的体积最大.
为何值时,储粮仓的体积最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com