
分析 (1)联立直线与抛物线方程,化为关于y的一元二次方程,由根与系数关系求出A,B两点的横纵坐标的和与积,直接运用数量积的坐标运算求解;
(2)直接代入三角形面积公式求解即可
解答 解:(1)设$A({-{y_1}^2,{y_1}})$,$B({-{y_2}^2,{y_2}})$由题意可知:k≠0,∴$x=-\frac{y}{k}+1$,
联立y2=-x得:ky2+y-k=0显然:△>0,
∴$\left\{\begin{array}{l}{{y}_{1}+{y}_{2}=-\frac{1}{k}}\\{{y}_{1}•{y}_{2}=-1}\end{array}\right.$,
∴$\overrightarrow{OA}•\overrightarrow{OB}$=(-y12)(-y22)+y1y2=(-1)2+1=0,
(2)∵S△OAB=$\frac{1}{2}$×1×|y1-y2|=$\frac{1}{2}$$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{1}{2}$$\sqrt{\frac{1}{{k}^{2}}+4}$=$\frac{5}{4}$,
解得:k=±$\frac{2}{3}$,
∴直线l的方程为:2x+3y+2=0或2x-3y+2=0.
点评 本题考查了直线和圆锥曲线的关系,考查了平面向量数量积的坐标运算,训练了三角形面积的求法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $2\sqrt{2}$ | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
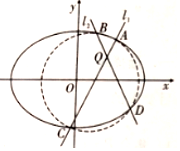 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>1})$中,a=$\sqrt{2}$b,且椭圆E上任一点到点$P({-\frac{1}{2},0})$的最小距离为$\frac{{\sqrt{7}}}{2}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>1})$中,a=$\sqrt{2}$b,且椭圆E上任一点到点$P({-\frac{1}{2},0})$的最小距离为$\frac{{\sqrt{7}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{256}$ | B. | $\frac{1}{128}$ | C. | $\frac{1}{64}$ | D. | $\frac{1}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}π$ | B. | $\frac{7}{3}π$ | C. | 2π | D. | $\frac{7}{2}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\sqrt{3)}$ | B. | $({1,\frac{{\sqrt{10}}}{2}}]$ | C. | (1,2) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
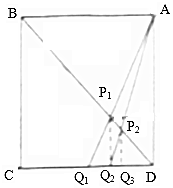 如图,已知ABCD是边长为1的正方形,Q1为CD的中点,Pi(i=1,2…,n)为AQi与BD的交点,过Pi作CD的垂线,垂足为Qi+1,则$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{5}{24}$.
如图,已知ABCD是边长为1的正方形,Q1为CD的中点,Pi(i=1,2…,n)为AQi与BD的交点,过Pi作CD的垂线,垂足为Qi+1,则$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{5}{24}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com