
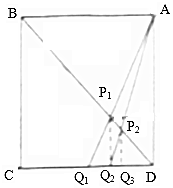
 如图,已知ABCD是边长为1的正方形,Q1为CD的中点,Pi(i=1,2…,n)为AQi与BD的交点,过Pi作CD的垂线,垂足为Qi+1,则$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{5}{24}$.
如图,已知ABCD是边长为1的正方形,Q1为CD的中点,Pi(i=1,2…,n)为AQi与BD的交点,过Pi作CD的垂线,垂足为Qi+1,则$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{5}{24}$. 分析 由题意可知:则A(1,1),Q1($\frac{1}{2}$,0),D(1,0),B(0,1),则直线BD:x+y=1,直线AQ:y=2x-1,求得P1($\frac{2}{3}$,$\frac{1}{3}$),则Q2($\frac{2}{3}$,0),则直线AQ2:y=3x-2,P2($\frac{3}{4}$,$\frac{1}{4}$),则Q3($\frac{3}{4}$,0),则Pi($\frac{i+1}{i+2}$,$\frac{1}{i+2}$),Qi($\frac{i}{i+1}$,0),根据三角形面积公式,${S}_{△D{Q}_{I}{P}_{I}}$=$\frac{1}{2}$丨DQi丨丨PiQi+1丨=$\frac{1}{2}$(1-$\frac{i}{i+1}$)×$\frac{1}{i+2}$=$\frac{1}{2}$($\frac{1}{i+1}$-$\frac{1}{i+2}$),采用“裂项法”即可求得$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$的值.
解答 解:如图,以C点为坐标原点,建立平面直角坐标系,由正方形ABCD边长为1,则A(1,1),Q1($\frac{1}{2}$,0),D(1,0),B(0,1),
则直线BD:x+y=1,直线AQ:y=2x-1,
联立可得P1($\frac{2}{3}$,$\frac{1}{3}$),则Q2($\frac{2}{3}$,0),
则直线AQ2:y=3x-2,
联立直线BD和直线AQ2,可得P2($\frac{3}{4}$,$\frac{1}{4}$),则Q3($\frac{3}{4}$,0),
…
可得Pi($\frac{i+1}{i+2}$,$\frac{1}{i+2}$),Qi($\frac{i}{i+1}$,0),
则${S}_{△D{Q}_{I}{P}_{I}}$=$\frac{1}{2}$丨DQi丨丨PiQi+1丨=$\frac{1}{2}$(1-$\frac{i}{i+1}$)×$\frac{1}{i+2}$=$\frac{1}{2}$($\frac{1}{i+1}$-$\frac{1}{i+2}$),
$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{1}{2}$$\sum_{i=1}^{10}$($\frac{1}{i+1}$-$\frac{1}{i+2}$),
=$\frac{1}{2}$[($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{11}$-$\frac{1}{12}$)],
=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{12}$),
=$\frac{5}{24}$,
则$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{5}{24}$,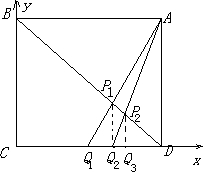
点评 本题考查三角形的面积公式,考查数列的应用,考查利用“裂项法”求数列的前n项和,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 144 | B. | 192 | C. | 360 | D. | 720 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com