
分析 首先分析题目因为n为正偶数,用数学归纳法证明的时候,若已假设n=k(k≥2,k为偶数)时命题为真时,因为n取偶数,则n=k+1代入无意义,故还需要证明n=k+2成立.
解答 解:用数学归纳法证明1-$\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{4}$+…-$\frac{1}{n}$=2($\frac{1}{n+2}$+$\frac{1}{n+4}$+…+$\frac{1}{2n}$)时
若已假设n=k(k≥2,k为偶数)时命题为真,因为n只能取偶数,所以还需要证明n=k+2成立.
故答案为:k+2.
点评 此题主要考查数学归纳法的概念问题,对学生的理解概念并灵活应用的能力有一定的要求,属于基础题目.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{256}$ | B. | $\frac{1}{128}$ | C. | $\frac{1}{64}$ | D. | $\frac{1}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\sqrt{3)}$ | B. | $({1,\frac{{\sqrt{10}}}{2}}]$ | C. | (1,2) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
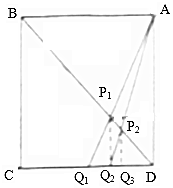 如图,已知ABCD是边长为1的正方形,Q1为CD的中点,Pi(i=1,2…,n)为AQi与BD的交点,过Pi作CD的垂线,垂足为Qi+1,则$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{5}{24}$.
如图,已知ABCD是边长为1的正方形,Q1为CD的中点,Pi(i=1,2…,n)为AQi与BD的交点,过Pi作CD的垂线,垂足为Qi+1,则$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{5}{24}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sum_{i=1}^{n}$(xi-a)最小 | B. | $\sum_{i=1}^{n}$|xi-a|最小 | ||
| C. | $\sum_{i=1}^{n}$(xi-a)2最小 | D. | $\frac{1}{n}$$\sum_{i=1}^{n}$|xi-a|最小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com