练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．在正项等比数列{an}中，a3=2，a4=8a7，则a9=（　　）
    A．$\frac{1}{256}$B．$\frac{1}{128}$C．$\frac{1}{64}$D．$\frac{1}{32}$

    分析 由等比数列的通项公式列出方程组，求出首项和公比，由此能求出结果．

    解答 解：∵正项等比数列{an}中，a3=2，a4=8a7，
    ∴$\left\{\begin{array}{l}{{a}_{3}={a}_{1}{q}^{2}=2}\\{{a}_{1}{q}^{3}=8{a}_{1}{q}^{6}}\\{q＞0}\end{array}\right.$，解得${a}_{1}=8，q=\frac{1}{2}$，
    a9=${a}_{1}{q}^{8}$=$\frac{1}{32}$．
    故选：D．

    点评 本题考查等比数列的第9项的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    20．已知函数f（x）=cosxsinx，给出下列四个结论：
    ①若f（x1）=-f（x2），则x1=-x2；
    ②f（x）的最小正周期是2π；
    ③f（x）在区间[-$\frac{π}{4}$，$\frac{π}{4}$]上是增函数；
    ④f（x）的图象关于直线x=$\frac{3π}{4}$对称．
    其中正确的结论是③④．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．设命题p：实数x满足x2-4ax+3a2＜0（a＞0），命题q：实数x满足$\frac{x-3}{x-2}≤0$．
    （1）若命题p的解集为P，命题q的解集为Q，当a=1时，求P∩Q；
    （2）若￢p是￢q的充分不必要条件，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

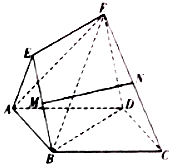    18．如图5所示，四边形ABCD是边长为2的正方形，四边形BDFE是平行四边形，点M，N分别是BE，CF的中点．
    （1）求证：MN∥平面ABCD；
    （2）若△ABE是等边三角形且平面ABE⊥平面ABCD，记三棱柱E-ABF的体积为S1，四棱锥F-ABCD的体积为S2，求$\frac{S_1}{S_2}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

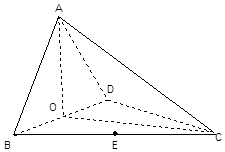    5．如图，四面体ABCD中，O、E分别是BD、BC的中点，底面BCD是正三角形，AC=BD=2，AB=AD=$\sqrt{2}$．
    （1）求异面直线AB与CD所成角的余弦值；
    （2）求点E到平面ACD的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知集合A={1，3，5}，B={3，5，7}，则A∪B={1，3，5，7}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知抛物线y2=-x与直线l：y=k（x+1）相交于A、B两点，点O为坐标原点．
    （1）求$\overrightarrow{OA}•\overrightarrow{OB}$的值；       
    （2）若△OAB的面积等于$\frac{5}{4}$，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知n为正偶数，用数学归纳法证明1-$\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{4}$+…-$\frac{1}{n}$=2（$\frac{1}{n+2}$+$\frac{1}{n+4}$+…+$\frac{1}{2n}$）时，若已假设n=k（k≥2且k为偶数）时等式成立，则还需要用归纳假设再证n=k+2时等式成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知一次函数f（x）在R上单调递增，当x∈[0，3]时，值域为[1，4]．
    （1）求函数f（x）的解析式；
    （2）当x∈[-1，8]时，求函数$g（x）=2x-\sqrt{f（x）}$的值域．

    查看答案和解析>>

    同步练习册答案