
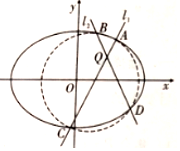 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>1})$中,a=$\sqrt{2}$b,且椭圆E上任一点到点$P({-\frac{1}{2},0})$的最小距离为$\frac{{\sqrt{7}}}{2}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>1})$中,a=$\sqrt{2}$b,且椭圆E上任一点到点$P({-\frac{1}{2},0})$的最小距离为$\frac{{\sqrt{7}}}{2}$.分析 (1)设M(x,y)为椭圆E上任一点,由$a=\sqrt{2}b$,椭圆E的方程可化为$\frac{x^2}{2}+{y^2}={b^2}$,通过求解椭圆E上任一点到点$P({-\frac{1}{2},0})$的最小距离为$\frac{{\sqrt{7}}}{2}$.即可求出椭圆的方程.
(2)直线l1,l2不重合,则直线l1,l2的斜率均存在,设直线l1:y=k(x-1)+1,点A(x1,y1),C(x2,y2).
直线l2:y=-k(x-1)+1.联立$\left\{\begin{array}{l}y=k({x-1})+1\\ \frac{x^2}{4}+\frac{y^2}{2}=1\end{array}\right.$消去y,由韦达定理以及弦长公式化简,可得|QA|•|QC|=|QB|•|QD|.
解答 (1)解:设M(x,y)为椭圆E上任一点,由$a=\sqrt{2}b$,
则椭圆E的方程可化为$\frac{x^2}{2}+{y^2}={b^2}$,
从而$|{MP}|=\sqrt{{{({x+\frac{1}{2}})}^2}+{y^2}}=\sqrt{{{({x+\frac{1}{2}})}^2}+{b^2}-\frac{x^2}{2}}=\sqrt{\frac{1}{2}{{({x+1})}^2}+{b^2}-\frac{1}{4}}$.
由于a>b>1,则当x=-1时,${|{MP}|_{min}}=\sqrt{{b^2}-\frac{1}{4}}=\frac{{\sqrt{7}}}{2}⇒{b^2}=2$,
故椭圆E的标准方程为$\frac{x^2}{4}+\frac{y^2}{2}=1$.
(2)证明:由于直线l1,l2不重合,则直线l1,l2的斜率均存在,
设直线l1:y=k(x-1)+1,点A(x1,y1),C(x2,y2).
易知直线l2:y=-k(x-1)+1.$|{QA}|•|{QC}|=\sqrt{1+{k^2}}•|{{x_1}-1}|•\sqrt{1+{k^2}}•|{{x_2}-1}|=({1+{k^2}})|{{x_1}{x_2}-({{x_1}+{x_2}})+1}|$,
由$\left\{\begin{array}{l}y=k({x-1})+1\\ \frac{x^2}{4}+\frac{y^2}{2}=1\end{array}\right.$得(1+2k2)x2+4k(1-k)x+2(1-k)2-4=0,
由韦达定理有:${x_1}+{x_2}=-\frac{{4k({1-k})}}{{1+2{k^2}}}$,${x_1}{x_2}=\frac{{2{{({1-k})}^2}-4}}{{1+2{k^2}}}$,
则$|{QA}|•|{QC}|=({1+{k^2}})|{\frac{{2{{({1-k})}^2}-4+4k({1-k})}}{{1+2{k^2}}}+1}|=\frac{{1+{k^2}}}{{1+2{k^2}}}$;
同理可得$|{QB}|•|{QD}|=\frac{{1+{{({-k})}^2}}}{{1+2{{({-k})}^2}}}=\frac{{1+{k^2}}}{{1+2{k^2}}}$,
从而有|QA|•|QC|=|QB|•|QD|.
点评 本题考查椭圆的方程的求法,椭圆的简单性质以及直线与椭圆的位置关系的综合应用,考查转化思想以及计算能力.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,3) | B. | (-4,2) | C. | (-4,3) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
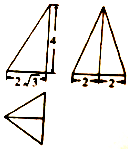 若一个几何体的三视图如图所示,则这个几何体的外接球的表面积为( )
若一个几何体的三视图如图所示,则这个几何体的外接球的表面积为( )| A. | 34π | B. | $\frac{80π}{3}$ | C. | $\frac{91}{3}π$ | D. | 114π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
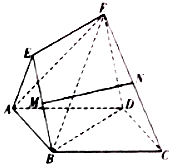 如图5所示,四边形ABCD是边长为2的正方形,四边形BDFE是平行四边形,点M,N分别是BE,CF的中点.
如图5所示,四边形ABCD是边长为2的正方形,四边形BDFE是平行四边形,点M,N分别是BE,CF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
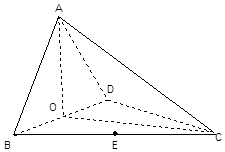 如图,四面体ABCD中,O、E分别是BD、BC的中点,底面BCD是正三角形,AC=BD=2,AB=AD=$\sqrt{2}$.
如图,四面体ABCD中,O、E分别是BD、BC的中点,底面BCD是正三角形,AC=BD=2,AB=AD=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com