
分析 (1)利用等差数列的通项公式即可得出;
(2)bn =$(\frac{1}{3})^{n+11}$+n,利用等差数列与等比数列的前n项和公式即可得出.
解答 解:(1)∵数列{an}对任意的n∈N*,满足an+1=an +1即an+1-an =1,a1=12.
∴数列{an}是等差数列,首项为12,公差为1.
∴an=12+(n-1)×1=n+11.
(2)bn =($\frac{1}{3}$)${\;}^{{a}_{n}}$+n=$(\frac{1}{3})^{n+11}$+n,
∴数列{bn}的前n项和=$\frac{(\frac{1}{3})^{12}[1-(\frac{1}{3})^{n}]}{1-\frac{1}{3}}$+$\frac{n(1+n)}{2}$
=$\frac{1}{2×{3}^{11}}$$[1-(\frac{1}{3})^{n}]$+$\frac{n(1+n)}{2}$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
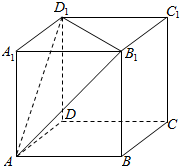 如图所示,正方体ABCD-A1B1C1D1的棱长为6,则以正方体ABCD-A1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为$24π+18\sqrt{2}π$.
如图所示,正方体ABCD-A1B1C1D1的棱长为6,则以正方体ABCD-A1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为$24π+18\sqrt{2}π$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
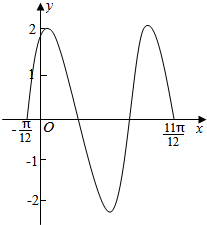 已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示:
已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
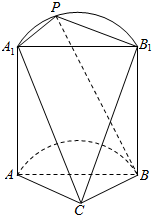 如图是一个半圆柱与多面体ABB1A1C构成的几何体,平面ABC与半圆柱的下底面共面,且AC⊥BC,P为$\widehat{{A}_{1}{B}_{1}}$上的动点.
如图是一个半圆柱与多面体ABB1A1C构成的几何体,平面ABC与半圆柱的下底面共面,且AC⊥BC,P为$\widehat{{A}_{1}{B}_{1}}$上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${C}_{4}^{3}$ | B. | ${P}_{4}^{3}$ | C. | ${4}_{\;}^{3}$ | D. | 34 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com