
分析 由新定义可得t的范围,验证可得最大的正整数n为4.
解答 解:若[t]=1,则t∈[1,2),
若[t2]=2,则t∈[$\sqrt{2}$,$\sqrt{3}$)(因为题目需要同时成立,则负区间舍去),
若[t3]=3,则t∈[$\root{3}{3}$,$\root{3}{4}$),
若[t4]=4,则t∈[$\root{4}{4}$,$\root{4}{5}$),
若[t5]=5,则t∈[$\root{5}{5}$,$\root{5}{6}$),
其中$\sqrt{3}$≈1.732,$\root{3}{4}$≈1.587,$\root{4}{5}$≈1.495,$\root{5}{6}$≈1.431<1.495,
通过上述可以发现,当t=4时,
可以找到实数t使其在区间[1,2)∩[$\sqrt{2}$,$\sqrt{3}$)∩[$\root{3}{3}$,$\root{3}{4}$)∩[$\root{4}{4}$,$\root{4}{5}$)上,
但当t=5时,无法找到实数t使其在区间[1,2)∩[$\sqrt{2}$,$\sqrt{3}$)∩[$\root{3}{3}$,$\root{3}{4}$)∩[$\root{4}{4}$,$\root{4}{5}$)∩[$\root{5}{5}$,$\root{5}{6}$)上,
∴正整数n的最大值4,
故答案为:4.
点评 本题考查简单的演绎推理,涉及新定义,属基础题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (1) | B. | (2) | C. | (3) | D. | (4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x<sinx且x>tanx | B. | ?x∈R,x≥sinx或x≤tanx | ||
| C. | ?x∈R,x<sinx或x>tanx | D. | ?x∈R,x≥sinx且x≤tanx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 用小正方体搭一个几何体,使得它的正视图和俯视图如图所示,这样的几何体只有一种吗?若不是,则这种几何体最少需要多少个小正方体?最多需要多少个小正方体?
用小正方体搭一个几何体,使得它的正视图和俯视图如图所示,这样的几何体只有一种吗?若不是,则这种几何体最少需要多少个小正方体?最多需要多少个小正方体?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
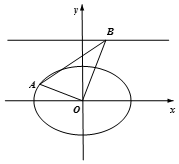 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),离心率为$\frac{{\sqrt{2}}}{2}$,左准线方程是x=-2,设O为原点,点A在椭圆C上,点B在直线y=2上,且OA⊥OB.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),离心率为$\frac{{\sqrt{2}}}{2}$,左准线方程是x=-2,设O为原点,点A在椭圆C上,点B在直线y=2上,且OA⊥OB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com