
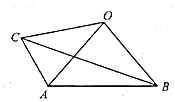
 如图,在四边形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )
如图,在四边形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )| A. | $\frac{13}{6}$ | B. | $\frac{8}{3}$ | C. | $\frac{17}{6}$ | D. | $\frac{13}{3}$ |
分析 建立坐标系,求出各点坐标,列方程组求出λ,μ的值即可得出答案.
解答 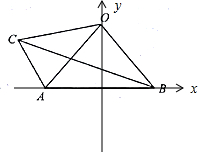 解:∵OA=BO=CO,∴O是△ABC的外接圆圆心,
解:∵OA=BO=CO,∴O是△ABC的外接圆圆心,
以AB为x轴,以AB的中点为原点建立坐标系,
则A(-1,0),B(1,0),C(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),
∴AB的中垂线方程为x=0,AC的中垂线方程为y-$\frac{\sqrt{3}}{4}$=$\frac{\sqrt{3}}{3}$(x+$\frac{5}{4}$),
联立方程组$\left\{\begin{array}{l}{x=0}\\{y-\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{3}(x+\frac{5}{4})}\end{array}\right.$,解得O(0,$\frac{2\sqrt{3}}{3}$),
∴$\overrightarrow{AO}$=(1,$\frac{2\sqrt{3}}{3}$),$\overrightarrow{AB}$=(2,0),$\overrightarrow{AC}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
∵$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,∴$\left\{\begin{array}{l}{2λ-\frac{1}{2}μ=1}\\{\frac{\sqrt{3}}{2}μ=\frac{2\sqrt{3}}{3}}\end{array}\right.$,
解得λ=$\frac{5}{6}$,μ=$\frac{4}{3}$.
∴λ+μ=$\frac{13}{6}$.
故选A.
点评 本题考查了平面向量的运算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>1} | B. | {x|x<1} | C. | {x|0<x<1} | D. | {x|x>1或x<-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
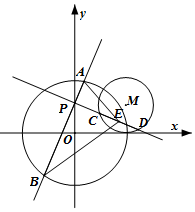 在平面直角坐标系xOy中,过点P(0,1)且互相垂直的两条直线分别与
在平面直角坐标系xOy中,过点P(0,1)且互相垂直的两条直线分别与查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,${x_0}^2+{x_0}+2017<0$ | B. | ?x∈R,x2+x+2017≤0 | ||
| C. | ?x0∈R,${x_0}^2+{x_0}+2017≤0$ | D. | ?x∈R,x2+x+2017>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
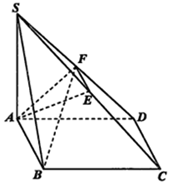 如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2,$AB=\sqrt{6}$
如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2,$AB=\sqrt{6}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{3}{2}$,+∞) | B. | (-∞,3)∪(3,+∞) | C. | [$\frac{3}{2}$,3)∪(3,+∞) | D. | (3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com